העולם שבו אנו חיים יפה בצורה בלתי נתפסת ומלא בתהליכים רבים ושונים שקובעים את מסלול החיים. כל התהליכים הללו נחקרים על ידי המדע המוכר - פיזיקה. זה מספק הזדמנות לקבל לפחות מושג כלשהו על מקור היקום. במאמר זה נשקול מושג כמו תיאוריה קינטית מולקולרית, המשוואות, הסוגים והנוסחאות שלה. עם זאת, לפני שתעבור למחקר מעמיק יותר של נושאים אלה, עליך להבהיר לעצמך את עצם המשמעות של הפיזיקה והתחומים שהיא חוקרת.
מהי פיזיקה?

למעשה, זהו מדע נרחב מאוד, ואולי, אחד המדעים הבסיסיים ביותר בהיסטוריה של האנושות. לדוגמה, אם אותו מדעי המחשב קשור כמעט לכל תחום של פעילות אנושית, בין אם זה עיצוב חישובי או יצירת קריקטורות, אז הפיזיקה היא החיים עצמם, תיאור התהליכים והזרימות המורכבות שלהם. בואו ננסה להבין את המשמעות שלו, לפשט את ההבנה ככל האפשר.
אזלפיכך, פיזיקה היא מדע העוסק בחקר אנרגיה וחומר, הקשרים ביניהם, הסבר של תהליכים רבים המתרחשים ביקום העצום שלנו. התיאוריה המולקולרית-קינטית של מבנה החומר היא רק טיפה קטנה בים התיאוריות וענפי הפיזיקה.
אנרגיה, שהמדע הזה לומד בפירוט, יכולה להיות מיוצגת במגוון צורות. לדוגמה, בצורה של אור, תנועה, כוח משיכה, קרינה, חשמל ועוד צורות רבות אחרות. ניגע במאמר זה בתיאוריה הקינטית המולקולרית של מבנה הצורות הללו.
חקר החומר נותן לנו מושג על המבנה האטומי של החומר. אגב, זה נובע מהתיאוריה המולקולרית-קינטית. מדע מבנה החומר מאפשר לנו להבין ולמצוא את משמעות קיומנו, את הסיבות להופעת החיים ואת היקום עצמו. בוא ננסה בכל זאת ללמוד את התיאוריה הקינטית המולקולרית של החומר.
ראשית, יש צורך במבוא כדי להבין במלואו את הטרמינולוגיה ואת כל המסקנות.
נושאים בפיזיקה
בתשובה לשאלה מהי תיאוריה מולקולרית-קינטית, אי אפשר שלא לדבר על חלקים בפיזיקה. כל אחד מאלה עוסק בלימוד והסבר מפורט של תחום מסוים בחיי האדם. הם מסווגים כדלקמן:
- מכניקה, המחולקת לשני חלקים נוספים: קינמטיקה ודינמיקה.
- סטטי.
- תרמודינמיקה.
- קטע מולקולרי.
- אלקטרודינמיקה.
- אופטיקה.
- פיזיקה של קוונטים וגרעין האטום.
בוא נדבר ספציפית על מולקולריתפיזיקה, כי היא מבוססת על התיאוריה המולקולרית-קינטית.
מהי תרמודינמיקה?
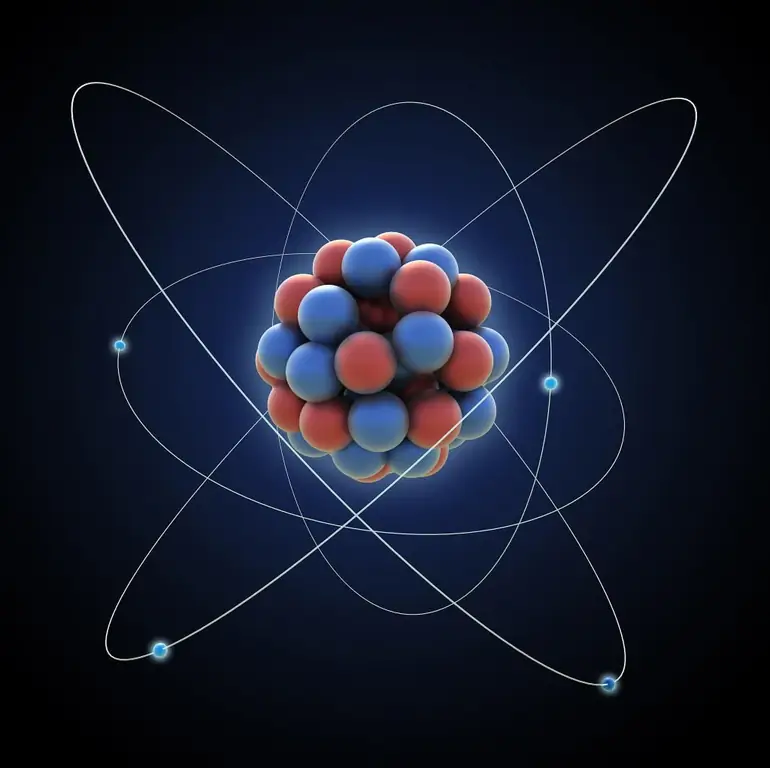
באופן כללי, החלק המולקולרי והתרמודינמיקה הם ענפים קרובים של הפיזיקה, החוקרים אך ורק את המרכיב המקרוסקופי של המספר הכולל של המערכות הפיזיקליות. כדאי לזכור שמדעים אלו מתארים במדויק את המצב הפנימי של גופים וחומרים. לדוגמה, מצבם במהלך חימום, התגבשות, אידוי ועיבוי, ברמה האטומית. במילים אחרות, פיזיקה מולקולרית היא מדע המערכות המורכבות ממספר עצום של חלקיקים: אטומים ומולקולות.
מדעים אלה הם שחקרו את ההוראות העיקריות של התיאוריה הקינטית המולקולרית.
גם במהלך כיתה ז', התוודענו למושגים של מיקרו ומקרו-עולמות, מערכות. לא יהיה מיותר לרענן מונחים אלה בזיכרון.
עולם המיקרו, כפי שאנו יכולים לראות מעצם שמו, מורכב מחלקיקים יסודיים. במילים אחרות, זהו עולם החלקיקים הקטנים. הגדלים שלהם נמדדים בטווח שבין 10-18 m ל-10-4 m, וזמן המצב האמיתי שלהם יכול להגיע גם לאינסוף וגם מרווחים קטנים באופן לא פרופורציונלי, לדוגמה, 10-20 s.
Macroworld מחשיב גופים ומערכות של צורות יציבות, המורכבות מחלקיקים יסודיים רבים. מערכות כאלה תואמות את הגודל האנושי שלנו.
בנוסף, יש דבר כזה מגה עולם. הוא מורכב מכוכבי לכת ענקיים, גלקסיות קוסמיות ומתחמים.
יסודותתיאוריה
עכשיו, לאחר שסיכמנו מעט ונזכרנו במונחים הבסיסיים של הפיזיקה, נוכל לעבור ישירות לנושא הראשי של מאמר זה.
תיאוריה מולקולרית-קינטית הופיעה ונוסחה לראשונה במאה התשע-עשרה. המהות שלו טמונה בעובדה שהוא מתאר בפירוט את המבנה של כל חומר (לעתים קרובות יותר מבנה של גזים מאשר גופים מוצקים ונוזליים), בהתבסס על שלוש הוראות יסוד שנאספו מהנחותיהם של מדענים בולטים כמו רוברט הוק, אייזק ניוטון, דניאל ברנולי, מיכאיל לומונוסוב ורבים אחרים.
ההוראות העיקריות של התיאוריה הקינטית המולקולרית נשמעים כך:
- לחלוטין לכל החומרים (ללא קשר אם הם נוזלים, מוצקים או גזים) יש מבנה מורכב, המורכב מחלקיקים קטנים יותר: מולקולות ואטומים. אטומים נקראים לפעמים "מולקולות יסוד".
- כל החלקיקים היסודיים האלה נמצאים תמיד במצב של תנועה מתמשכת וכאוטית. כל אחד מאיתנו נתקל בהוכחה ישירה להצעה זו, אך, ככל הנראה, לא ייחס לה חשיבות רבה. לדוגמה, כולנו ראינו על רקע קרני השמש שחלקיקי אבק נעים כל הזמן בכיוון כאוטי. זה נובע מהעובדה שהאטומים מייצרים דחיפות הדדיות זה עם זה, ומעניקים כל הזמן אנרגיה קינטית זה לזה. תופעה זו נחקרה לראשונה ב-1827, והיא נקראה על שמו של המגלה - "תנועה בראון".
- כל החלקיקים היסודיים נמצאים בתהליך של אינטראקציה מתמשכת זה עם זהכוחות מסוימים שיש להם סלע חשמלי.
ראוי לציין שדוגמה נוספת המתארת עמדה מספר שתיים, שעשויה לחול, למשל, גם על התיאוריה הקינטית המולקולרית של גזים, היא דיפוזיה. אנו נתקלים בזה בחיי היומיום, ובמספר בדיקות ובקרות, לכן חשוב שיהיה לנו מושג לגביו.
תחילה, שקול את הדוגמאות הבאות:
הרופא שפך בטעות אלכוהול מבקבוק על השולחן. או שאולי הפלת את בקבוק הבושם שלך והוא התפשט על כל הרצפה.
מדוע, בשני המקרים הללו, גם ריח האלכוהול וגם ריח הבושם ימלאו את כל החדר לאחר זמן מה, ולא רק את האזור שבו נשפכה תכולת החומרים הללו?
התשובה פשוטה: דיפוזיה.
דיפוזיה - מה זה? איך זה זורם?

זהו תהליך שבו החלקיקים המרכיבים חומר מסוים (בדרך כלל גז) חודרים לתוך החללים הבין-מולקולריים של אחר. בדוגמאות שלנו למעלה, התרחשו הדברים הבאים: עקב תנועה תרמית, כלומר תנועה מתמשכת ומפורקת, מולקולות אלכוהול ו/או בושם נפלו למרווחים בין מולקולות האוויר. בהדרגה, בהשפעת התנגשות עם אטומים ומולקולות אוויר, הם התפשטו ברחבי החדר. אגב, עוצמת הדיפוזיה, כלומר מהירות זרימתה, תלויה בצפיפות החומרים המעורבים בדיפוזיה, וכן באנרגיית התנועה של האטומים והמולקולות שלהם, הנקראת קינטית. ככל שהאנרגיה הקינטית גדולה יותר, כך המהירות של מולקולות אלו גבוהות יותר, בהתאמה, והעוצמה.
תהליך הדיפוזיה המהיר ביותר יכול להיקרא דיפוזיה בגזים. זאת בשל העובדה שהגז אינו הומוגני בהרכבו, כלומר חללים בין-מולקולריים בגזים תופסים כמות משמעותית של מקום, בהתאמה, ותהליך הכנסת אטומים ומולקולות של חומר זר לתוכם מתנהל קל ומהיר יותר..
תהליך זה מעט איטי יותר בנוזלים. המסת קוביות סוכר בספל תה היא רק דוגמה להתפשטות של מוצק בנוזל.
אבל הזמן הארוך ביותר הוא דיפוזיה בגופים בעלי מבנה גבישי מוצק. זה בדיוק כך, מכיוון שמבנה המוצקים הוא הומוגני ויש לו סריג גבישי חזק, שבתאיו רוטטים האטומים של המוצק. לדוגמה, אם מנקים היטב את המשטחים של שני מוטות מתכת ואז מביאים זה לזה מגע, אז לאחר זמן מספיק ארוך נוכל לזהות חתיכות של מתכת אחת בשנייה, ולהיפך.
כמו כל סעיף יסודי אחר, התיאוריה הבסיסית של הפיזיקה מחולקת לחלקים נפרדים: סיווג, טיפוסים, נוסחאות, משוואות וכן הלאה. לפיכך, למדנו את היסודות של התיאוריה הקינטית המולקולרית. זה אומר שאתה יכול להמשיך בבטחה לבחינת בלוקים תיאורטיים בודדים.
תיאוריה מולקולרית-קינטית של גזים
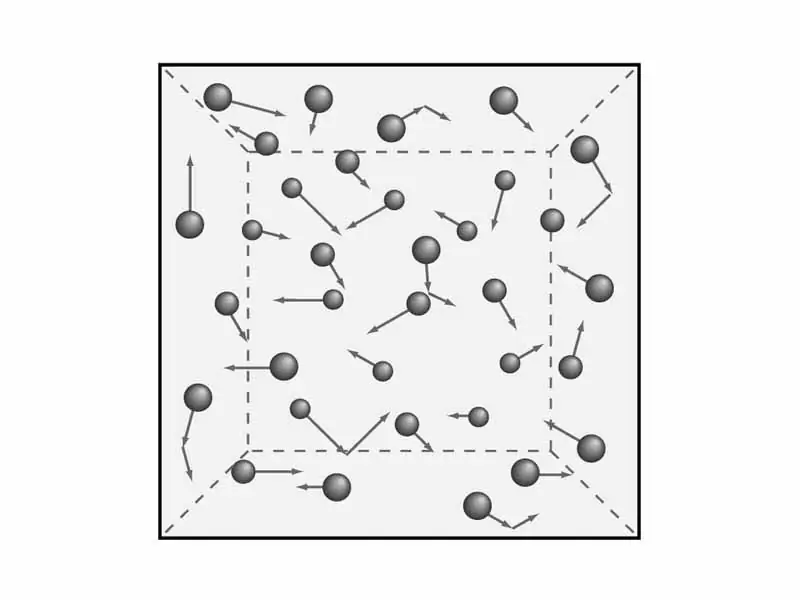
יש צורך להבין את הוראות תורת הגז. כפי שאמרנו קודם, נשקול את המאפיינים המקרוסקופיים של גזים, כגון לחץ וטמפרטורה. זהיהיה צורך מאוחר יותר על מנת לגזור את המשוואה של התיאוריה המולקולרית-קינטית של הגזים. אבל מתמטיקה - מאוחר יותר, ועכשיו בואו נעסוק בתיאוריה ובהתאם, בפיזיקה.
מדענים ניסחו חמישה סעיפים של התיאוריה המולקולרית של גזים, המשמשים להבנת המודל הקינטי של גזים. הם נשמעים כך:
- כל הגזים מורכבים מחלקיקים יסודיים שאין להם גודל מסוים, אבל בעלי מסה מסוימת. במילים אחרות, נפחם של חלקיקים אלו הוא מינימלי בהשוואה לאורך ביניהם.
- לאטומים ולמולקולות של גזים אין כמעט אנרגיה פוטנציאלית, בהתאמה, לפי החוק, כל האנרגיה שווה לקינטית.
- כבר הכרנו את העמדה הזו קודם - תנועה בראונית. כלומר, חלקיקי גז נמצאים תמיד בתנועה רציפה וכאוטית.
- לחלוטין כל ההתנגשויות ההדדיות של חלקיקי גז, המלוות במסר של מהירות ואנרגיה, הן אלסטיות לחלוטין. המשמעות היא שאין איבוד אנרגיה או קפיצות חדות באנרגיה הקינטית שלהם במהלך התנגשות.
- בתנאים רגילים וטמפרטורה קבועה, האנרגיה הממוצעת של תנועת החלקיקים של כמעט כל הגזים זהה.
נוכל לשכתב את המיקום החמישי באמצעות משוואה מסוג זה של התיאוריה המולקולרית-קינטית של הגזים:
E=1/2mv^2=3/2kT, כאשר k הוא קבוע בולצמן; T - טמפרטורה בקלווין.
משוואה זו גורמת לנו להבין את הקשר בין המהירות של חלקיקי גז אלמנטריים לבין הטמפרטורה המוחלטת שלהם. בהתאם, ככל שהמוחלט שלהם גבוה יותרטמפרטורה, ככל שהמהירות והאנרגיה הקינטית שלהם גדולים יותר.
לחץ גז
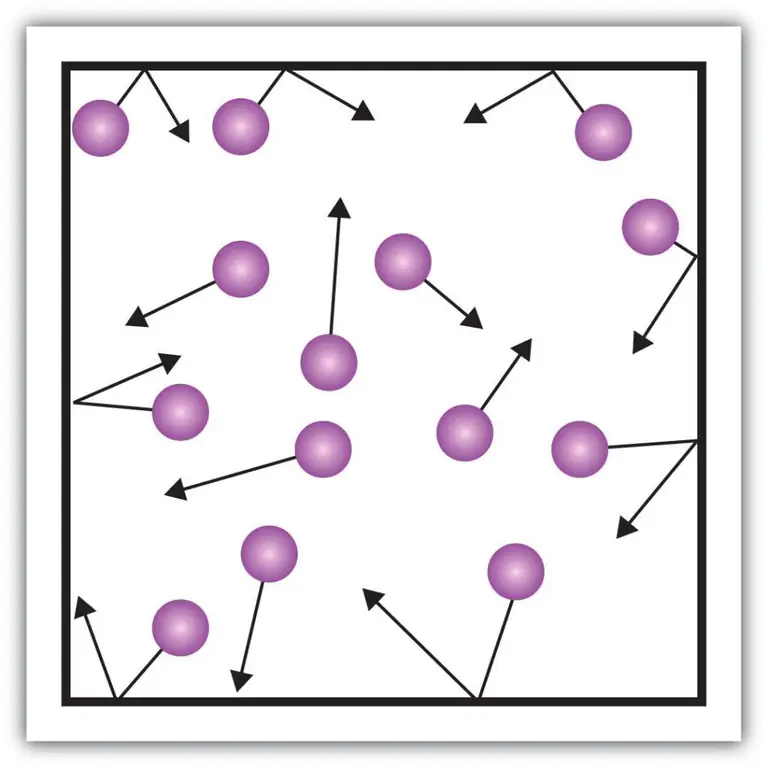
ניתן להסביר רכיבים מקרוסקופיים כאלה של המאפיין, כמו לחץ של גזים, גם באמצעות התיאוריה הקינטית. כדי לעשות זאת, נדמיין את הדוגמה הבאה.
בוא נניח שמולקולה של גז כלשהו נמצאת בקופסה, שאורכה הוא L. הבה נשתמש בהוראות תורת הגזים שתוארו לעיל וניקח בחשבון את העובדה שהכדור המולקולרי נע רק לאורך ה-x -צִיר. כך, נוכל לצפות בתהליך ההתנגשות האלסטית באחד מדפנות הכלי (קופסה).
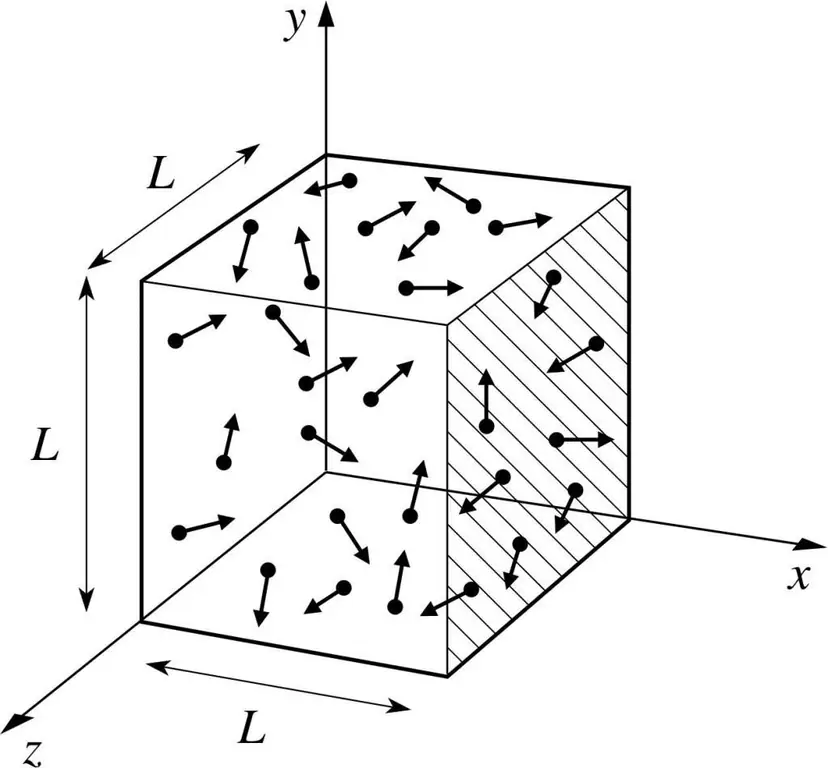
המומנטום של ההתנגשות המתמשכת, כידוע, נקבע על ידי הנוסחה: p=mv, אבל במקרה זה, נוסחה זו תלבש צורת השלכה: p=mv(x).
מכיוון שאנו מתייחסים רק לממד של ציר ה-x, כלומר ציר ה-x, השינוי הכולל בתנע יבוא לידי ביטוי בנוסחה: mv(x) - m(-v(x))=2mv(x).
לאחר מכן, שקול את הכוח המופעל על ידי האובייקט שלנו באמצעות החוק השני של ניוטון: F=ma=P/t.
מהנוסחאות האלה אנו מבטאים את הלחץ מצד הגז: P=F/a;
עכשיו בואו נחליף את ביטוי הכוח בנוסחה המתקבלת ונקבל: P=mv(x)^2/L^3.
לאחר מכן, ניתן לכתוב את נוסחת הלחץ המוגמרת שלנו עבור המספר ה-N של מולקולות הגז. במילים אחרות, זה ייראה כך:
P=Nmv(x)^2/V, כאשר v הוא מהירות ו-V הוא נפח.
עכשיו בואו ננסה להדגיש כמה הוראות בסיסיות בנושא לחץ גז:
- זה מתבטא דרךהתנגשויות של מולקולות עם מולקולות של דפנות העצם שבו הוא נמצא.
- גודל הלחץ עומד ביחס ישר לכוח ולמהירות הפגיעה של מולקולות על דפנות הכלי.
כמה מסקנות קצרות על תיאוריה
לפני שנלך רחוק יותר ונבחן את המשוואה הבסיסית של התיאוריה הקינטית המולקולרית, אנו מציעים לך כמה מסקנות קצרות מהנקודות ומהתיאוריה שלעיל:
- המדד של אנרגיית התנועה הממוצעת של האטומים והמולקולות שלו היא הטמפרטורה המוחלטת.
- כאשר שני גזים שונים נמצאים באותה טמפרטורה, למולקולות שלהם יש אותה אנרגיה קינטית ממוצעת.
- האנרגיה של חלקיקי גז עומדת ביחס ישר למהירות הריבועית הממוצעת: E=1/2mv^2.
- למרות שלמולקולות הגז יש אנרגיה קינטית ממוצעת, בהתאמה, ומהירות ממוצעת, חלקיקים בודדים נעים במהירויות שונות: חלקם מהירים, חלקם איטיים.
- ככל שהטמפרטורה גבוהה יותר, כך מהירות המולקולות גבוהה יותר.
- כמה פעמים אנחנו מעלים את טמפרטורת הגז (לדוגמה, כפול), אנרגיית התנועה של החלקיקים שלו גדלה פי כמה (בהתאמה, מכפילה).
משוואה ונוסחאות בסיסיות

המשוואה הבסיסית של התיאוריה הקינטית המולקולרית מאפשרת לקבוע את הקשר בין הכמויות של עולם המיקרו ובהתאם, הכמויות המקרוסקופיות, כלומר הנמדדות.
אחד המודלים הפשוטים ביותר שהתיאוריה המולקולרית יכולה לשקול הוא מודל הגז האידיאלי.
אפשר להגיד את זהזהו סוג של מודל דמיוני שנחקר על ידי התיאוריה הקינטית המולקולרית של גז אידיאלי, שבו:
- חלקיקי הגז הפשוטים ביותר נחשבים ככדורים אלסטיים לחלוטין המקיימים אינטראקציה הן זה עם זה והן עם מולקולות הדפנות של כל כלי רק במקרה אחד - התנגשות אלסטית לחלוטין;
- כוחות המשיכה בתוך הגז נעדרים, או שבעצם אפשר להזניח אותם;
- ניתן לקחת אלמנטים של המבנה הפנימי של הגז כנקודות חומריות, כלומר, ניתן גם להזניח את נפחם.
בהתחשב במודל כזה, הפיזיקאי יליד גרמניה רודולף קלאוזיוס כתב נוסחה ללחץ גז דרך היחס בין פרמטרים מיקרו- ומקרוסקופיים. זה נראה כמו:
p=1/3m(0)nv^2.
מאוחר יותר תקרא נוסחה זו כמשוואה הבסיסית של התיאוריה המולקולרית-קינטית של גז אידיאלי. זה יכול להיות מוצג בכמה צורות שונות. חובתנו כעת היא להציג קטעים כמו פיזיקה מולקולרית, תיאוריה קינטית מולקולרית, ומכאן את המשוואות והסוגים השלמים שלהם. לכן, הגיוני לשקול וריאציות אחרות של הנוסחה הבסיסית.
אנו יודעים שניתן למצוא את האנרגיה הממוצעת המאפיינת את תנועת מולקולות הגז באמצעות הנוסחה: E=m(0)v^2/2.
במקרה זה, נוכל להחליף את הביטוי m(0)v^2 בנוסחת הלחץ המקורית באנרגיה הקינטית הממוצעת. כתוצאה מכך, תהיה לנו הזדמנות לחבר את המשוואה הבסיסית של התיאוריה הקינטית המולקולרית של גזים בצורה הבאה: p=2/3nE.
חוץ מזה, כולנו יודעים שניתן לכתוב את הביטוי m(0)n כמכפלה של שתי מנות:
m/NN/V=m/V=ρ.
לאחר המניפולציות האלה, נוכל לשכתב את הנוסחה שלנו למשוואה של התיאוריה המולקולרית-קינטית של גז אידיאלי בצורה שלישית ושונה:
p=1/3ρv^2.
ובכן, אולי זה כל מה שאתה צריך לדעת בנושא זה. נותר רק לעשות שיטתיות של הידע שנצבר בצורה של מסקנות קצרות (ולא כך).
כל המסקנות והנוסחאות הכלליות בנושא "תיאוריה מולקולרית-קינטית"
אז בואו נתחיל.
ראשון:
פיזיקה הוא מדע יסוד הנכלל במהלך מדעי הטבע, החוקר את תכונות החומר והאנרגיה, המבנה שלהם, דפוסי הטבע האנאורגניים.
זה כולל את הסעיפים הבאים:
- מכניקה (קינמטיקה ודינמיקה);
- static;
- תרמודינמיקה;
- electrodynamics;
- קטע מולקולרי;
- אופטיקה;
- פיסיקה של הקוונטים וגרעין האטום.
שני:
פיזיקה של חלקיקים ותרמודינמיקה הם ענפים קרובים החוקרים את המרכיב המקרוסקופי הבלעדי של המספר הכולל של המערכות הפיזיקליות, כלומר, מערכות המורכבות ממספר עצום של חלקיקים יסודיים.
הם מבוססים על תיאוריה קינטית מולקולרית.
Third:
עיקר העניין הוא זה. התיאוריה הקינטית המולקולרית מתארת בפירוט את המבנה של חומר (לעתים קרובות יותר מבנה של גזים מאשר מוצקים).וגופים נוזליים), המבוססים על שלוש הנחות יסוד שנאספו מהנחותיהם של מדענים בולטים. ביניהם: רוברט הוק, אייזק ניוטון, דניאל ברנולי, מיכאיל לומונוסוב ורבים אחרים.
רביעי:
שלושה עקרונות בסיסיים של תיאוריה קינטית מולקולרית:
- לכל החומרים (ללא קשר אם הם נוזלים, מוצקים או גזים) יש מבנה מורכב המורכב מחלקיקים קטנים יותר: מולקולות ואטומים.
- כל החלקיקים הפשוטים האלה נמצאים בתנועה כאוטית מתמשכת. דוגמה: תנועה ודיפוזיה בראונית.
- כל המולקולות בכל תנאי פועלות ביניהן עם כוחות מסוימים שיש להם סלע חשמלי.
כל אחד מההוראות האלה של התיאוריה הקינטית המולקולרית מהווה בסיס איתן בחקר מבנה החומר.
חמישי:
מספר נקודות עיקריות של התיאוריה המולקולרית עבור מודל הגז:
- כל הגזים מורכבים מחלקיקים יסודיים שאין להם גודל מסוים, אבל בעלי מסה מסוימת. במילים אחרות, נפחם של חלקיקים אלו הוא מינימלי בהשוואה למרחקים ביניהם.
- לאטומים ולמולקולות של גזים אין כמעט אנרגיה פוטנציאלית, בהתאמה, האנרגיה הכוללת שלהם שווה לזו הקינטית.
- כבר הכרנו את העמדה הזו קודם - תנועה בראונית. כלומר, חלקיקי גז נמצאים תמיד בתנועה רציפה ואקראית.
- לחלוטין כל ההתנגשויות ההדדיות של אטומים ומולקולות של גזים, המלוות במסר של מהירות ואנרגיה, הן אלסטיות לחלוטין. זהפירושו שאין איבוד אנרגיה או קפיצות חדות באנרגיה הקינטית שלהם במהלך התנגשות.
- בתנאים רגילים וטמפרטורה קבועה, האנרגיה הקינטית הממוצעת של כמעט כל הגזים זהה.
שישי:
מסקנות מהתיאוריה על גזים:
- טמפרטורה אבסולוטית היא מדד לאנרגיה הקינטית הממוצעת של האטומים והמולקולות שלה.
- כאשר שני גזים שונים נמצאים באותה טמפרטורה, למולקולות שלהם יש אותה אנרגיה קינטית ממוצעת.
- האנרגיה הקינטית הממוצעת של חלקיקי גז עומדת ביחס ישר למהירות הריבוע הממוצעת של השורש: E=1/2mv^2.
- למרות שלמולקולות הגז יש אנרגיה קינטית ממוצעת, בהתאמה, ומהירות ממוצעת, חלקיקים בודדים נעים במהירויות שונות: חלקם מהירים, חלקם איטיים.
- ככל שהטמפרטורה גבוהה יותר, כך מהירות המולקולות גבוהה יותר.
- כמה פעמים אנחנו מעלים את טמפרטורת הגז (לדוגמה, כפול), גם האנרגיה הקינטית הממוצעת של חלקיקיו עולה כל כך הרבה פעמים (בהתאמה, מכפילה).
- היחס בין הלחץ של גז על דפנות הכלי שבו הוא נמצא לבין עוצמת הפגיעה של מולקולות על דפנות אלה הוא פרופורציונלי ישר: ככל שהשפעות רבות יותר, כך הלחץ גבוה יותר, ולהיפך.
שביעית:
מודל גז אידיאלי הוא מודל שבו יש לעמוד בתנאים הבאים:
- מולקולות גז יכולות ונחשבות ככדורים אלסטיים לחלוטין.
- כדורים אלה יכולים לקיים אינטראקציה זה עם זה ועם הקירות של כל אחדכלי שיט רק במקרה אחד - התנגשות אלסטית לחלוטין.
- הכוחות המתארים את הדחף ההדדי בין אטומים ומולקולות של גז נעדרים או שניתן למעשה להזניח אותם.
- אטומים ומולקולות נחשבים כנקודות חומריות, כלומר, ניתן גם להזניח את נפחם.
שמיני:
בוא ניתן את כל המשוואות הבסיסיות ונראה את הנוסחאות בנושא "תיאוריה מולקולרית-קינטית":
p=1/3m(0)nv^2 - המשוואה הבסיסית למודל הגז האידיאלי, נגזרת על ידי הפיזיקאי הגרמני רודולף קלאוזיוס.
p=2/3nE - המשוואה הבסיסית של התיאוריה המולקולרית-קינטית של גז אידיאלי. נגזר מהאנרגיה הקינטית הממוצעת של המולקולות.
р=1/3ρv^2 - אותה משוואה, אך נחשבת דרך הצפיפות והמהירות המרובעת הממוצעת של מולקולות גז אידיאליות.
m(0)=M/N(a) - הנוסחה למציאת המסה של מולקולה אחת דרך מספר האבוגדרו.
v^2=(v(1)+v(2)+v(3)+…)/N - נוסחה למציאת המהירות הריבועית הממוצעת של מולקולות, כאשר v(1), v(2), v (3) וכן הלאה - המהירות של המולקולה הראשונה, השנייה, השלישית וכן הלאה עד למולקולה ה-n.
n=N/V - נוסחה למציאת ריכוז המולקולות, כאשר N הוא מספר המולקולות בנפח גז לנפח נתון V.
E=mv^2/2=3/2kT - נוסחאות למציאת האנרגיה הקינטית הממוצעת של מולקולות, כאשר v^2 הוא השורש הממוצע של המהירות הריבועית של מולקולות, k הוא קבוע ערך על שם האוסטרי הפיזיקה של לודוויג בולצמן, ו-T הוא טמפרטורת הגז.
p=nkT - נוסחת לחץ מבחינת ריכוז, קבועבולצמן והטמפרטורה המוחלטת T. ממנה נובעת נוסחה יסודית נוספת, שהתגלתה על ידי המדען הרוסי מנדלייב והפיזיקאי-מהנדס הצרפתי קלייפרון:
pV=m/MRT, כאשר R=kN(a) הוא הקבוע האוניברסלי לגזים.
עכשיו בואו נראה קבועים עבור תהליכי איזו שונים: איזוברי, איזוחורי, איזותרמי ואדיאבטי.
pV/T=const - מבוצע כאשר המסה והרכב הגז קבועים.
рV=const - אם גם הטמפרטורה קבועה.
V/T=const - אם לחץ הגז קבוע.
p/T=const - אם עוצמת הקול קבועה.
אולי זה כל מה שאתה צריך לדעת בנושא זה.
היום צללנו לתחום מדעי כמו פיזיקה תיאורטית, על המקטעים והבלוקים המרובים שלה. ביתר פירוט, נגענו בתחום כזה של הפיזיקה כמו פיזיקה מולקולרית בסיסית ותרמודינמיקה, דהיינו, תיאוריה מולקולרית-קינטית, אשר, כך נראה, אינה מציגה קשיים במחקר הראשוני, אך למעשה יש לה מלכודות רבות.. זה מרחיב את הבנתנו את מודל הגז האידיאלי, שגם אותו למדנו בפירוט. בנוסף, ראוי לציין שגם הכרנו את המשוואות הבסיסיות של התיאוריה המולקולרית על הווריאציות השונות שלהן, וכן שקלנו את כל הנוסחאות הנחוצות ביותר למציאת כמויות מסוימות לא ידועות בנושא זה.זה יהיה שימושי במיוחד בעת הכנה לכתיבה כל מבחנים, בחינות ומבחנים, או כדי להרחיב את ההשקפה הכללית והידע של הפיזיקה.
אנו מקווים שהמאמר הזה היה שימושי עבורך, ושאבת ממנו רק את המידע הדרוש ביותר, מחזקת את הידע שלך בעמודי התווך של התרמודינמיקה כמו ההוראות הבסיסיות של התיאוריה הקינטית המולקולרית.






