הנושא של המאמר של היום שלנו יהיה הקינמטיקה של נקודה חומרית. במה מדובר? אילו מושגים מופיעים בו ואיזו הגדרה יש לתת למונח זה? ננסה לענות על שאלות אלו ועוד רבות אחרות היום.
הגדרה ומושג
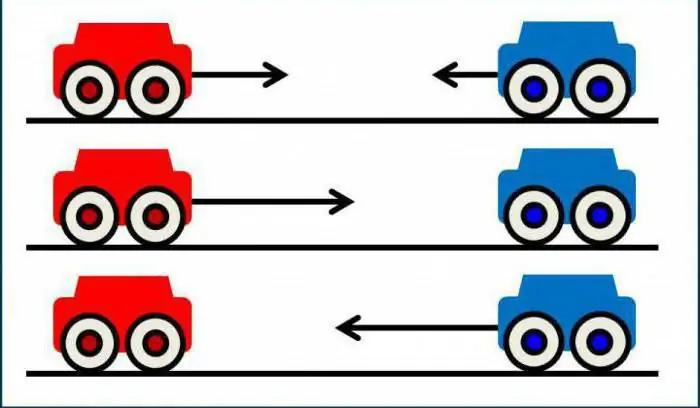
קינמטיקה של נקודה חומרית היא לא יותר מאשר תת-סעיף של הפיזיקה שנקרא "מכניקה". היא, בתורה, חוקרת את דפוסי התנועה של גופים מסוימים. הקינמטיקה של נקודה חומרית עוסקת גם בבעיה זו, אך אינה עושה זאת באופן כללי. למעשה, תת-סעיף זה בוחן שיטות המאפשרות לך לתאר את תנועת הגוף. במקרה זה, רק הגופים הנקראים אידיאלים מתאימים למחקר. אלה כוללים: נקודה חומרית, גוף קשיח לחלוטין וגז אידיאלי. בואו נשקול את המושגים ביתר פירוט. כולנו יודעים מספסל הלימודים כי נהוג לקרוא לנקודה חומרית גוף אשר ניתן להזניח את מידותיו במצב נתון. אגב, הקינמטיקה של תנועת התרגום של נקודה חומרית מתחילה לראשונהמופיעים בספרי לימוד פיזיקה לכיתה ז'. זהו הענף הפשוט ביותר, ולכן הכי נוח להתחיל היכרות עם המדע בעזרתו. שאלה נפרדת היא מהם מרכיבי הקינמטיקה של נקודה חומרית. יש די הרבה מהם, ובתנאי שניתן לחלק אותם לכמה רמות עם מורכבות שונה להבנה. אם אנחנו מדברים, למשל, על וקטור הרדיוס, אז, באופן עקרוני, אין שום דבר מסובך באופן איסור בהגדרתו. עם זאת, תסכימו שלתלמיד יהיה הרבה יותר קל להבין זאת מאשר לתלמיד בחטיבת הביניים או התיכון. ולמען האמת, אין צורך להסביר את המאפיינים של המונח הזה לתלמידי תיכון.
היסטוריה קצרה של יצירת הקינמטיקה
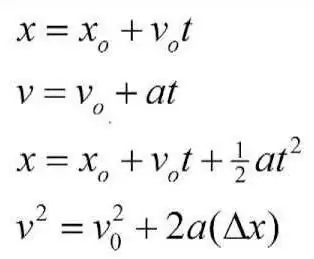
לפני שנים רבות, המדען הדגול אריסטו הקדיש את חלק הארי מזמנו הפנוי לחקר ולתיאור הפיזיקה כמדע נפרד. הוא גם עבד על קינמטיקה, וניסה להציג את התזות והמושגים העיקריים שלה, בדרך זו או אחרת בשימוש בניסיונות לפתור בעיות מעשיות ואפילו יומיומיות. אריסטו נתן את הרעיונות הראשוניים לגבי מה הם מרכיבי הקינמטיקה של נקודה חומרית. יצירותיו ויצירותיו יקרות מאוד עבור כל האנושות. אף על פי כן, במסקנותיו הוא עשה מספר לא מבוטל של טעויות, והסיבה לכך היו תפיסות מוטעות וחישובים שגויים. בשלב מסוים, מדען אחר, גלילאו גליליי, התעניין בעבודותיו של אריסטו. אחת התזות היסודיות שהעלה אריסטו הייתה שתנועת הגוףמתרחש רק אם הוא מופעל על ידי כוח כלשהו, הנקבע על ידי עוצמה וכיוון. גלילאו הוכיח שזו טעות. הכוח ישפיע על פרמטר מהירות התנועה, אך לא יותר. האיטלקי הראה שכוח הוא הגורם לתאוצה, והוא יכול להתעורר רק יחד איתו. כמו כן, גלילאו גליליי הקדיש תשומת לב רבה לחקר תהליך הנפילה החופשית, תוך גזירת הדפוסים המתאימים. כנראה שכולם זוכרים את הניסויים המפורסמים שלו, שערך על המגדל הנטוי של פיזה. הפיזיקאי אמפר השתמש גם ביסודות הפתרונות הקינמטיים בעבודותיו.
מושגים ראשוניים
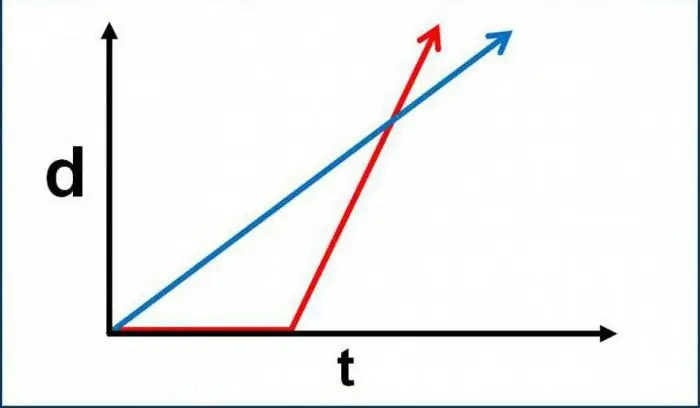
כפי שהוזכר קודם לכן, קינמטיקה היא חקר דרכים לתאר את התנועה של עצמים בעלי אידיאליזציה. במקרה זה, ניתן ליישם בפועל את היסודות של ניתוח מתמטי, אלגברה רגילה וגיאומטריה. אבל אילו מושגים (דווקא מושגים, ולא הגדרות לכמויות פרמטריות) עומדים בבסיס תת-סעיף זה של הפיזיקה? ראשית, כולם צריכים להבין בבירור שהקינמטיקה של תנועת התרגום של נקודה חומרית מתייחסת לתנועה מבלי לקחת בחשבון אינדיקטורים של כוח. כלומר, כדי לפתור את הבעיות המתאימות, אין לנו צורך בנוסחאות הקשורות לכוח. זה לא נלקח בחשבון על ידי הקינמטיקה, לא משנה כמה מהם יש - אחד, שניים, שלושה, לפחות כמה מאות אלפים. עם זאת, קיומה של האצה עדיין מסופק. במספר בעיות, הקינמטיקה של התנועה של נקודה חומרית קובעת את גודל התאוצה. עם זאת, הגורמים לתופעה זו (כלומר, הכוחות וטבעם) אינם נחשבים אלא מושמטים.
Classification
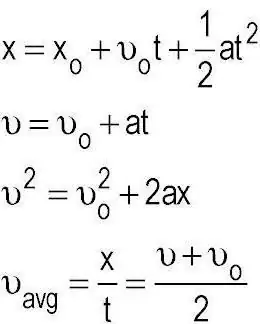
גילינו שהקינמטיקה חוקרת ומיישמת שיטות לתיאור תנועת גופים ללא קשר לכוחות הפועלים עליהם. אגב, תת-סעיף נוסף של מכניקה, שנקרא דינמיקה, עוסק במשימה כזו. כבר שם מיושמים חוקי ניוטון, המאפשרים בפועל לקבוע לא מעט פרמטרים עם כמות קטנה של נתונים ראשוניים ידועים. המושגים הבסיסיים של הקינמטיקה של נקודה חומרית הם מרחב וזמן. ובקשר להתפתחות המדע הן בכלל והן בתחום זה, עלתה השאלה לגבי ההתאמה של שימוש בשילוב כזה.
מההתחלה הייתה קינמטיקה קלאסית. אנו יכולים לומר שהוא מאופיין לא רק בנוכחותם של פערים זמניים ומרחביים כאחד, אלא גם בעצמאותם מבחירה של מסגרת התייחסות כזו או אחרת. אגב, נדבר על זה קצת מאוחר יותר. עכשיו בואו רק נסביר על מה אנחנו מדברים. במקרה זה, קטע ייחשב למרווח מרחבי, ומרווח זמן ייחשב למרווח זמני. הכל נראה ברור. אז, פערים אלה ייחשבו בקינמטיקה הקלאסית כמוחלטים, בלתי משתנים, במילים אחרות, בלתי תלויים במעבר ממסגרת התייחסות אחת לאחרת. בין אם קינמטיקה רלטיבית עסקית. בה, הפערים במהלך המעבר בין מערכות ייחוס יכולים להשתנות. זה אפילו יותר נכון לומר שהם לא יכולים, אבל הם חייבים, כנראה. בגלל זה, בו זמנית של השנייםאירועים אקראיים הופכים גם הם ליחסיים ונתונים לשיקול מיוחד. לכן בקינמטיקה רלטיביסטית שני מושגים - מרחב וזמן - משולבים לאחד.
קינמטיקה של נקודה חומרית: מהירות, תאוצה וכמויות אחרות
כדי להבין לפחות קצת את תת הסעיף הזה של הפיזיקה, צריך לנווט בין המושגים החשובים ביותר, להכיר את ההגדרות ולדמיין מהי כמות כזו או אחרת במונחים כלליים. אין בזה שום דבר קשה, למעשה, הכל מאוד קל ופשוט. שקול, אולי, מלכתחילה, את המושגים הבסיסיים המשמשים בבעיות קינמטיקה.
Movement
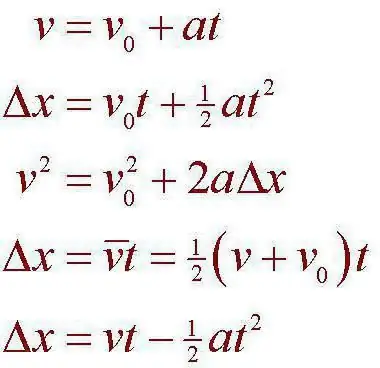
תנועה מכנית נשקול את התהליך שבמהלכו אובייקט אידיאלי כזה או אחר משנה את מיקומו במרחב. במקרה זה, ניתן לומר שהשינוי מתרחש ביחס לגופים אחרים. כמו כן, יש צורך לקחת בחשבון את העובדה כי הקמת מרווח זמן מסוים בין שני אירועים מתרחשת בו זמנית. כך למשל, ניתן יהיה לבודד מרווח מסוים שנוצר במהלך הזמן שחלף בין הגעת הגוף ממצב אחד למשנהו. אנו גם מציינים כי הגופים במקרה זה יכולים ויעשו אינטראקציה זה עם זה, על פי חוקי המכניקה הכלליים. זה בדיוק מה שהקינמטיקה של נקודה חומרית פועלת לרוב. מערכת ההתייחסות היא המושג הבא שקשור איתה באופן בלתי נפרד.
קואורדינטות
ניתן לקרוא להם נתונים רגילים המאפשרים לקבוע את מיקום הגוף בזמן זה או אחר. קואורדינטות קשורות קשר בל יינתק עם הרעיון של מערכת ייחוס, כמו גם לרשת הקואורדינטות. לרוב הם שילוב של אותיות ומספרים.
Radius vector
מהשם כבר אמור להיות ברור מה זה. עם זאת, בואו נדבר על זה ביתר פירוט. אם נקודה נעה לאורך מסלול מסוים, ואנו יודעים בדיוק את ההתחלה של מערכת ייחוס מסוימת, אז נוכל לצייר וקטור רדיוס בכל עת. הוא יחבר את המיקום ההתחלתי של הנקודה למיקום המיידי או הסופי.
מסלול
זה ייקרא קו רציף, אשר מונח כתוצאה מתנועה של נקודה חומרית במערכת ייחוס מסוימת.
Speed (גם ליניארי וגם זוויתי)
זהו ערך שיכול לדעת כמה מהר הגוף עובר מרווח מרחק מסוים.
האצה (זוויתית וליניארית)
מראה לפי איזה חוק ובאיזו עוצמה משתנה פרמטר המהירות של הגוף.
אולי, הנה הם - המרכיבים העיקריים של הקינמטיקה של נקודה חומרית. יש לציין שגם מהירות וגם תאוצה הם כמויות וקטוריות. וזה אומר שיש להם לא רק ערך אינדיקטיבי כלשהו, אלא גם כיוון מסוים. אגב, אפשר לכוון אותם גם לכיוון אחד וגם לכיוונים מנוגדים. במקרה הראשון, הגוף יאיץ, במקרה השני הוא יאט.
משימות פשוטות
קינמטיקה של נקודה חומרית (מהירות, תאוצה ומרחק שבהם הם מושגים בסיסיים למעשה) כוללת לא רק מספר עצום של משימות, אלא הרבה מהקטגוריות השונות שלהן. בואו ננסה לפתור בעיה פשוטה למדי על ידי קביעת המרחק שעבר הגוף.
נניח שהתנאים העומדים לרשותנו הם כדלקמן. מכונית הנהג נמצאת בקו הזינוק. המפעיל נותן את האישור עם הדגל, והמכונית ממריאה בפתאומיות. קבע אם היא יכולה לקבוע שיא חדש בתחרות המרוצים, אם המובילה הבאה עברה מרחק של מאה מטר ב-7.8 שניות. קח את התאוצה של המכונית שווה ל-3 מטרים חלקי שנייה בריבוע.
אז, איך לפתור את הבעיה הזו? זה די מעניין, מכיוון שאנו נדרשים לא "לייבש" לקבוע פרמטרים מסוימים. זה מתבהר עם תחליפים ומצב מסוים, שמגוון את תהליך הפתרון והחיפוש אחר אינדיקטורים. אבל במה עלינו להיות מודרכים לפני שניגשים למשימה?
1. הקינמטיקה של נקודה חומרית מספקת את השימוש בתאוצה במקרה זה.
2. הפתרון מבוסס על שימוש בנוסחת המרחק, שכן ערכה המספרי מופיע בתנאים.
הבעיה נפתרה למעשה בפשטות. לשם כך, ניקח את נוסחת המרחק: S=VoT + (-) AT ^ 2/2. מה הפואנטה? עלינו לברר כמה זמן יעבור הרוכב את המרחק המיועד, ולאחר מכן להשוות את הנתון לשיא כדי לגלות אם הוא מנצח אותו או לא. לשם כך, הקצו זמן, נקבל את הנוסחהעבורו: AT^2 + 2VoT - 2S. זו לא יותר ממשוואה ריבועית. אבל המכונית ממריאה, מה שאומר שהמהירות ההתחלתית תהיה 0. כשפותרים את המשוואה, המבחין יהיה שווה ל-2400. כדי למצוא את השעה, צריך להוריד את השורש. בוא נעשה את זה למקום העשרוני השני: 48.98 מצא את שורש המשוואה: 48.98/6=8.16 שניות. מסתבר שהנהג לא יוכל לנצח את השיא הקיים.






