לימוד תכונותיו של גז אידיאלי הוא נושא חשוב בפיזיקה. מבוא למאפיינים של מערכות גז מתחיל בבחינה של משוואת בויל-מריוט, שכן זהו החוק הראשון שהתגלה בניסוי של גז אידיאלי. בואו נשקול את זה ביתר פירוט במאמר.
מה הכוונה בגז אידיאלי?
לפני שנדבר על חוק בויל-מריוט והמשוואה שמתארת אותו, בואו נגדיר גז אידיאלי. נהוג להבין את זה כחומר נוזלי שבו החלקיקים המרכיבים אותו אינם מקיימים אינטראקציה זה עם זה, וגדליהם קטנים באופן זניח בהשוואה למרחקים הבין-חלקיקים הממוצעים.
למעשה, כל גז הוא אמיתי, כלומר, לאטומים ולמולקולות המרכיבים אותו יש גודל מסוים ואינם מקיימים אינטראקציה זה עם זה בעזרת כוחות ואן דר ואלס. עם זאת, בטמפרטורות מוחלטות גבוהות (יותר מ-300 K) ובלחצים נמוכים (פחות מאטמוספירה אחת), האנרגיה הקינטית של אטומים ומולקולות גבוהה בהרבה מהאנרגיה של אינטראקציות ואן דר ואלס, כך שהגז האמיתי בנקודה המצוינתתנאים בעלי דיוק גבוה יכולים להיחשב אידיאלים.
משוואת בויל-מריוט
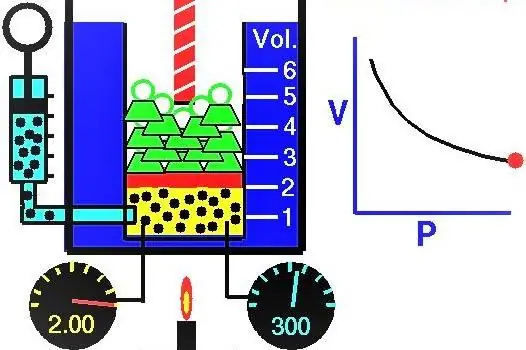
מאפיינים של גזים מדענים אירופאים חקרו באופן פעיל במהלך המאות XVII-XIX. חוק הגז הראשון שהתגלה בניסוי היה החוק המתאר את התהליכים האיזוטרמיים של התפשטות ודחיסה של מערכת גז. ניסויים מקבילים בוצעו על ידי רוברט בויל ב-1662 ואדם מריוטה ב-1676. כל אחד מהמדענים הללו הראה באופן עצמאי שבמהלך תהליך איזותרמי במערכת גז סגורה, הלחץ משתנה הפוך לנפח. הביטוי המתמטי שהתקבל בניסוי של התהליך כתוב בצורה הבאה:
PV=k
כאשר P ו-V הם הלחץ במערכת ונפחה, k הוא קבוע כלשהו, שערכו תלוי בכמות חומר הגז ובטמפרטורה שלו. אם תבנה את התלות של פונקציית P(V) בגרף, זו תהיה היפרבולה. דוגמה של עקומות אלה מוצגת להלן.
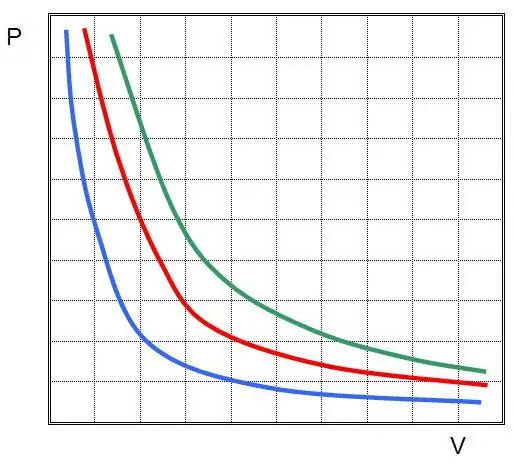
השוויון הכתוב נקרא משוואת בויל-מריוט (חוק). ניתן לנסח חוק זה בקצרה כך: התפשטות גז אידיאלי בטמפרטורה קבועה מביאה לירידה פרופורציונלית בלחץ בו, להיפך, דחיסה איזותרמית של מערכת גז מלווה בעלייה פרופורציונלית בלחץ בה.
משוואת הגז האידיאלית
חוק בויל-מריוט הוא מקרה מיוחד של חוק כללי יותר הנושא את שמותיהם של מנדלייב וקלפיירון. אמיל קלפיירון, המסכם את המידע הניסיוני על התנהגות גזים בתנאים חיצוניים שונים, השיג בשנת 1834 את המשוואה הבאה:
PV=nRT
במילים אחרות, המכפלה של נפח V של מערכת גז והלחץ P בה עומדים ביחס ישר למכפלת הטמפרטורה המוחלטת T וכמות החומר n. מקדם המידתיות הזה מסומן באות R ונקרא קבוע הגז האוניברסלי. במשוואה הכתובה הופיע ערכו של R עקב החלפת מספר קבועים, שנעשתה על ידי דמיטרי איבנוביץ' מנדלייב בשנת 1874.
ממשוואת המצב האוניברסלית קל לראות שהקביעות של הטמפרטורה וכמות החומר מבטיחות את השונות של הצד הימני של המשוואה, מה שאומר שגם הצד השמאלי של המשוואה יישאר קבוע. במקרה זה, נקבל את משוואת בויל-מריוט.

חוקי גז אחרים
משוואת Clapeyron-Mendeleev שנכתבה בפסקה למעלה מכילה שלושה פרמטרים תרמודינמיים: P, V ו-T. אם כל אחד מהם קבוע, ולשני האחרים מותר להשתנות, אז נקבל את Boyle-Mariotte, משוואות צ'ארלס וגיי-לוסאק. חוק צ'ארלס מדבר על מידתיות ישירה בין נפח וטמפרטורה לתהליך איזוברי, וחוק גאי-לוסאק קובע שבמקרה של מעבר איזוחורי, לחץ הגז עולה או יורד ביחס ישר לטמפרטורה המוחלטת. המשוואות המתאימות נראות כך:
V/T=const כאשר P=const;
P/T=const כאשר V=const.
אזלפיכך, חוק בויל-מריוט הוא אחד משלושת חוקי הגז העיקריים. עם זאת, היא שונה מהשאר מבחינת התלות הגרפית: הפונקציות V(T) ו-P(T) הן קווים ישרים, הפונקציה P(V) היא היפרבולה.
דוגמה למשימה ליישום חוק בויל-מריוט
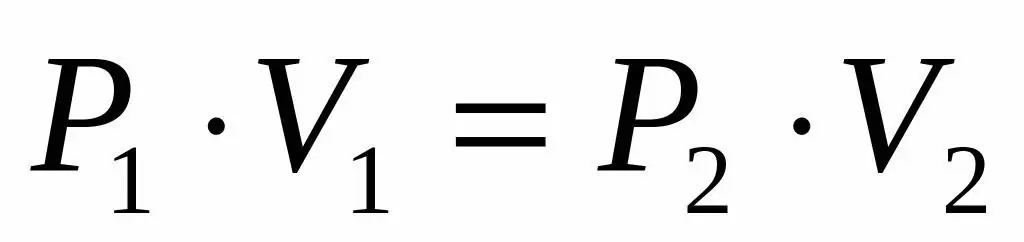
נפח הגז בצילינדר מתחת לבוכנה במצב ההתחלתי היה 2 ליטר, והלחץ שלו היה 1 אטמוספירה. מה היה לחץ הגז לאחר עליית הבוכנה ונפח מערכת הגז גדל ב-0.5 ליטר. התהליך נחשב לאיזוטרמי.
מכיוון שניתן לנו את הלחץ והנפח של גז אידיאלי, ואנחנו גם יודעים שהטמפרטורה נשארת ללא שינוי במהלך התפשטותו, נוכל להשתמש במשוואת בויל-מריוט בצורה הבאה:
P1V1=P2V 2
השוויון הזה אומר שתוצר הנפח-לחץ הוא קבוע עבור כל מצב של הגז בטמפרטורה נתונה. הבעת הערך P2 מתוך שוויון, נקבל את הנוסחה הסופית:
P2=P1V1/V 2
בעת ביצוע חישובי לחץ, אתה יכול להשתמש ביחידות מחוץ למערכת במקרה זה, מכיוון שהליטרים יתכווצו, ונקבל את הלחץ P2באטמוספרות. בהחלפת הנתונים מהתנאי, נגיע לתשובה לשאלת הבעיה: P2=0.8 אטמוספרות.






