תופעות הטבע והתהליכים סביבנו מורכבים למדי. לתיאור הפיזי המדויק שלהם, יש להשתמש במנגנון מתמטי מסורבל ולקחת בחשבון מספר רב של גורמים משמעותיים. כדי למנוע בעיה זו, משתמשים בכמה מודלים מפושטים בפיזיקה, אשר מקלים מאוד על הניתוח המתמטי של התהליך, אך למעשה אינם משפיעים על דיוק התיאור שלו. אחד מהם הוא דגם הגז האידיאלי. בואו נשקול את זה ביתר פירוט במאמר.
המושג של גז אידיאלי
גז אידיאלי הוא מצב צבירה של חומר, המורכב מנקודות חומר שאינן מקיימות אינטראקציה זו עם זו. הבה נסביר את ההגדרה הזו ביתר פירוט.
ראשית, אנחנו מדברים על נקודות חומריות כעצמים המרכיבים גז אידיאלי. זה אומר שלמולקולות ולאטומים שלו אין גודל, אלא יש להם מסה מסוימת. זה נועזניתן לעשות קירוב תוך התחשבות בעובדה שבכל הגזים האמיתיים בלחצים נמוכים וטמפרטורות גבוהות, המרחק בין מולקולות גדול בהרבה מהממדים הליניאריים שלהן.
שנית, המולקולות בגז אידיאלי לא אמורות לקיים אינטראקציה זו עם זו. במציאות, אינטראקציות כאלה תמיד קיימות. אז אפילו אטומים של גזים אצילים חווים משיכה דיפול-דיפול. במילים אחרות, קיימות אינטראקציות של ואן דר ואלס. עם זאת, בהשוואה לאנרגיה הקינטית של סיבוב ותנועה טרנסלציונית של מולקולות, אינטראקציות אלה כה קטנות עד שהן אינן משפיעות על תכונות הגזים. לכן, לא ניתן להתייחס אליהם בעת פתרון בעיות מעשיות.
חשוב לציין שלא כל הגזים בהם הצפיפות נמוכה והטמפרטורה גבוהה יכולים להיחשב אידיאלים. בנוסף לאינטראקציות של ואן דר ואלס, ישנם סוגים אחרים וחזקים יותר של קשרים, למשל קשרי מימן בין מולקולות H2O, שמובילים להפרה גסה של תנאי האידיאליות של הגז. מסיבה זו, אדי מים אינם גז אידיאלי, אבל אוויר כן.
מודל פיזי של גז אידיאלי
ניתן לייצג את המודל הזה באופן הבא: נניח שמערכת הגז מכילה N חלקיקים. אלה יכולים להיות אטומים ומולקולות של כימיקלים ויסודות שונים. מספר ה-N חלקיקים גדול, כך שבדרך כלל משתמשים ביחידת "שומה" לתיאורה (שומה אחת מתאימה למספר של אבוגדרו). כולם נעים בנפח V כלשהו. תנועות חלקיקיםהם כאוטיים ובלתי תלויים זה בזה. לכל אחד מהם יש מהירות מסוימת v והוא נע לאורך נתיב ישר.
באופן תיאורטי, ההסתברות להתנגשות בין חלקיקים היא כמעט אפס, מכיוון שגודלם קטן בהשוואה למרחקים בין החלקיקים. עם זאת, אם מתרחשת התנגשות כזו, אז היא אלסטית לחלוטין. במקרה האחרון, התנע הכולל של החלקיקים והאנרגיה הקינטית שלהם נשמרים.
המודל הנחשב של גזים אידיאליים הוא מערכת קלאסית עם מספר עצום של אלמנטים. לכן, המהירות והאנרגיה של החלקיקים בו מצייתים להתפלגות הסטטיסטית של מקסוול-בולצמן. לחלקיקים מסוימים יש מהירויות נמוכות, בעוד שלאחרים יש מהירויות גבוהות. במקרה זה, יש מגבלת מהירות צרה מסוימת, שבה נמצאים הערכים הסבירים ביותר של כמות זו. התפלגות המהירות של מולקולות חנקן מוצגת באופן סכמטי להלן.
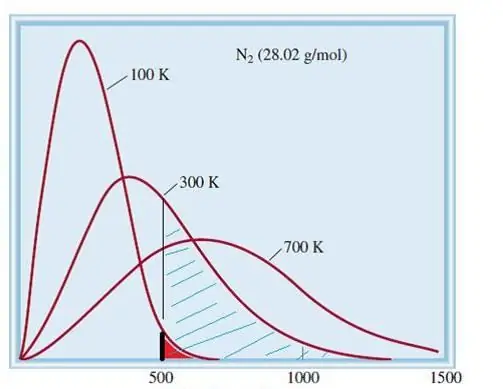
תיאוריה קינטית של גזים
מודל הגזים האידיאליים שתואר לעיל קובע באופן ייחודי את תכונות הגזים. דגם זה הוצע לראשונה על ידי דניאל ברנולי בשנת 1738.

לאחר מכן, הוא פותח למצבו הנוכחי על ידי אוגוסט קרוניג, רודולף קלאוסיוס, מיכאיל לומונוסוב, ג'יימס מקסוול, לודוויג בולצמן, מריאן סמולוצ'ובסקי ומדענים נוספים.
התיאוריה הקינטית של חומרים נוזליים, שעל בסיסה נבנה מודל הגז האידיאלי, מסבירה שתי תכונות מקרוסקופיות חשובות של המערכת בהתבסס על התנהגותה המיקרוסקופית:
- הלחץ בגזים הוא תוצאה של התנגשות של חלקיקים עם קירות הכלי.
- הטמפרטורה במערכת היא תוצאה של ביטוי של תנועה מתמדת של מולקולות ואטומים.
בואו נרחיב על שתי המסקנות של התיאוריה הקינטית.
לחץ גז
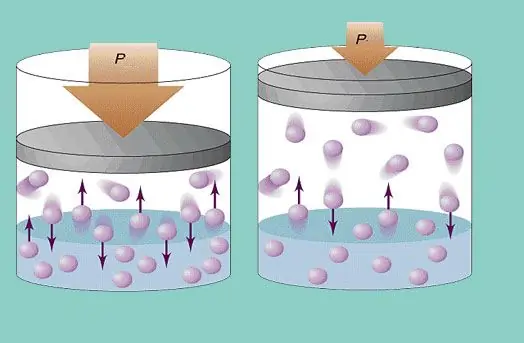
מודל הגז האידיאלי מניח תנועה כאוטית מתמדת של חלקיקים במערכת והתנגשות מתמדת שלהם עם קירות הכלי. כל התנגשות כזו נחשבת אלסטית לחלוטין. מסת החלקיקים קטנה (≈10-27-10-25 ק ג). לכן, הוא לא יכול ליצור לחץ רב בהתנגשות. אף על פי כן, מספר החלקיקים, ומכאן גם מספר ההתנגשויות, הוא עצום (≈1023). בנוסף, מהירות הריבוע הממוצעת של היסודות היא כמה מאות מטרים בשנייה בטמפרטורת החדר. כל זה מוביל ליצירת לחץ ניכר על קירות הכלי. ניתן לחשב אותו באמצעות הנוסחה הבאה:
P=Nmvcp2 / (3V), כאשר vcp הוא מהירות מרובעת ממוצעת של השורש, m היא מסת החלקיקים.
טמפרטורה אבסולוטית
לפי מודל הגז האידיאלי, הטמפרטורה נקבעת באופן ייחודי על ידי האנרגיה הקינטית הממוצעת של מולקולה או אטום במערכת הנחקרת. אתה יכול לכתוב את הביטוי הבא המקשר אנרגיה קינטית וטמפרטורה מוחלטת עבור גז אידיאלי:
mvcp2 / 2=3 / 2kB T.
כאן kB הוא קבוע בולצמן. מהשוויון הזה אנחנו מקבלים:
T=m vcp2 / (3kB).
משוואה אוניברסלית של המדינה
אם נשלב את הביטויים לעיל עבור לחץ מוחלט P וטמפרטורה מוחלטת T, נוכל לכתוב את השוויון הבא:
PV=nRT.
כאן n היא כמות החומר בשומות, R הוא קבוע הגז המוכנס על ידי D. I. Mendeleev. ביטוי זה הוא המשוואה החשובה ביותר בתורת הגזים האידיאליים, מכיוון שהוא משלב שלושה פרמטרים תרמודינמיים (V, P, T) ואינו תלוי במאפיינים הכימיים של מערכת הגז.

המשוואה האוניברסלית נגזרה לראשונה בניסוי על ידי הפיזיקאי הצרפתי אמיל קלפיירון במאה ה-19 ולאחר מכן הובאה לצורתה המודרנית על ידי הכימאי הרוסי מנדלייב, וזו הסיבה שהיא נושאת כיום את שמות המדענים הללו.






