ככל שהתלמידים מתבגרים, כך יש צורך במהירות בפתרון בעיות פשוטות. לא ניתן הרבה זמן בבחינות כדי לפתור דוגמאות או בעיות פשוטות לאורך זמן. איך למצוא את האלכסון של ריבוע במהירות ובקלות? את זה מלמדים ילדים מכיתה ח'. מאמר זה מציג שתי דרכים - אחת ארוכה יותר, השנייה מהירה יותר.
איך לחשב את האלכסון של ריבוע?
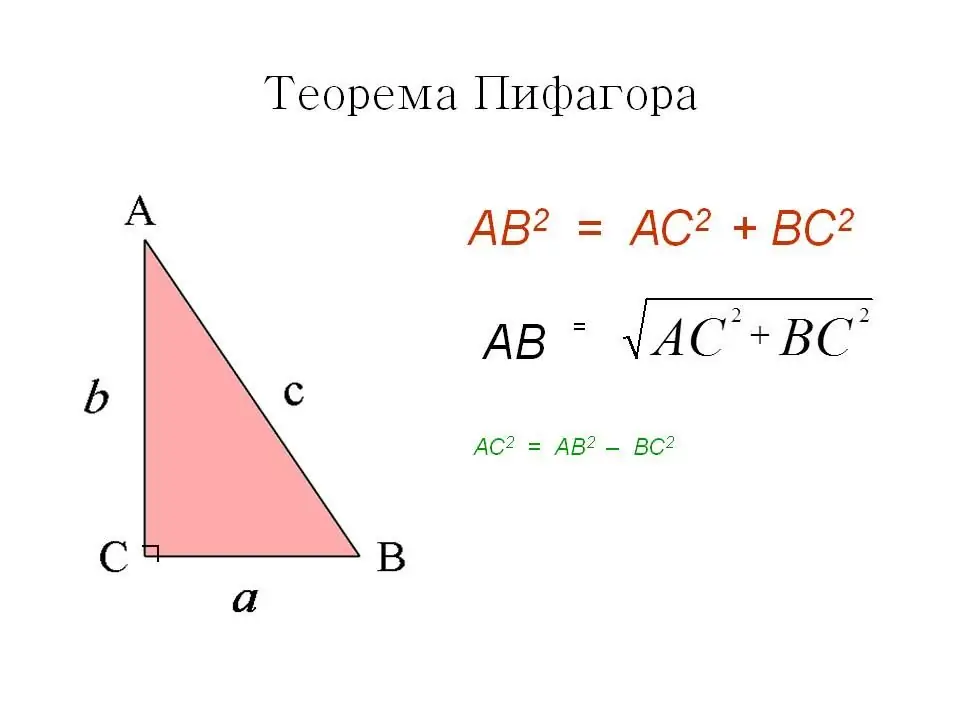
הדרך הראשונה היא משפט פיתגורס הידוע והמוכר. בריבוע, כל הזוויות ישרות, מה שאומר שהאלכסון מחלק אותו לשני משולשים ישרי זווית שווים והוא עצמו התחתון שלהם. על פי משפט פיתגורס, ריבוע התחתון שווה לסכום ריבועי הרגליים.

הדרך השנייה היא נוסחה פשוטה שייחודית לריבועים, ואתה רק צריך לזכור אותה. כידוע, כל צלעות הריבוע שוות, ולכן מתמטיקאים חישבו את הנוסחה הבאה למציאת האלכסון שלו: הוא שווה למכפלת הצלע והשורש של שתיים.
כמובן, עדיף פשוט לזכור את הנוסחה של אורך האלכסון של ריבוע ולהשתמש בה תמיד, כי זה הרבה יותר מהיר ונוח. זה מורגש במיוחד כשפותרים בעיות בצורה מילולית, שבה במקום ביטויי שורש גדולים שלמים, אפשר להסתדר עם מוצר אחד בלבד.
דוגמה
קח, למשל, ריבוע של 6 על 6, כלומר עם צלע השווה לשישה סנטימטרים.
לפי השיטה הראשונה: האלכסון יהיה C, והצד יהיה A.
אז נקבל ש-C=√A^2+A^2 או C=√2A^2.
בוא נכתוב את זה בצורה מספרית: С=√36 + 36. קיבלנו √72, שזה 3√8 או 6√2.
ועכשיו בואו נמצא את אותו אלכסון, אבל בשיטה השנייה: C=A√2 או בצורה מספרית: 6√2
עכשיו אפשר לראות עד כמה השיטה השנייה מהירה יותר, קלה יותר והכי חשוב - יעילה יותר, במיוחד בבעיות קלות כאלה, כי כל דקה יקרה בבחינה!
מאפיינים אחרים של אלכסונים מרובעים
מלבד לדעת איך למצוא את האלכסונים של ריבוע, צריך גם לדעת את המאפיינים שלהם. העיקריים שבהם הם:
- האלכסונים שווים זה לזה ונקודת החיתוך מחולקת לשניים.
- הם יוצרים זוויות ישרות כשהם מצטלבים.
- חלק את הריבוע למשולשים שווים.
מסקנה
השאלה כיצד לספור את האלכסונים של ריבוע נשאלת בדרך כלל על ידי תלמידים שפספסו נושא זה בבית הספר. עם זאת, כולם צריכים לדעת כללים בסיסיים כאלה של מתמטיקה! רצוי לפתור כמה שיותר מהר, וזה מצריך ידע בנוסחאות מקוצרות. כל זה מאוד פשוט וקל, אבליחד עם זאת, זהו הבסיס הדרוש לפתרון בעיות מורכבות הרבה יותר בעתיד. וחלק חשוב מהבסיס הזה הוא הריבוע.






