במתמטיקה, סיכום (מסומן בסמל הסיגמה היווני הגדול) הוא קבוצה של סיכומים של מספרים. מה הסכום? זו התוצאה של פעולה כזו. אם המספרים מתווספים אחד אחרי השני משמאל לימין, תוצאת הביניים היא סכום חלקי.
מהו הסכום?
המספרים שיש לסכם יכולים להיות מספר שלם, רציונלי, ממשי או מורכב. בנוסף אליהם, ניתן להוסיף סוגים נוספים של ערכים: וקטורים, מטריצות, פולינומים, ובכלל אלמנטים של כל קבוצה מתווספת (או אפילו מונואיד).
אם מספר האלמנטים של המונחים הוא סופי, אז הסיכום תמיד נותן ערך מוגדר היטב. סיכום של רצף אינסופי של ערכים נקרא סדרה. לעתים קרובות ניתן לקבוע את ערכו באמצעות גבול (אם כי לפעמים הערך יכול להיות אינסופי).
Sequences
ניתן להגדיר את סיכום המספרים [3, 7, 2, 1] על ידי ביטוי שערכו הוא סכום הספרות הכלולות בו, למשל 3 + 7 + 2 + 1=13. חיבורמבחינה אסוציאטיבית, הסכום אינו תלוי באופן שבו המונחים מקובצים, למשל, (3 + 7) + (2 + 1) ו-3 + ((7 + 2) + 1) שניהם שווים לתשעה, כך שבדרך כלל פוסלים על סוגריים. חיבור הוא גם קומוטטיבי, כך שסידור מחדש של המונחים אינו משנה את ערך הסכום. שים לב שייתכן שמאפיין זה לא יעבוד עבור סיכום אינסופי.

אין סימון מיוחד לסיכום רצפים מהסוג הזה. יש רק ניואנס קל אם יש פחות משני אלמנטים. הסיכום של רצף של איבר אחד אינו מכיל סימן פלוס (אין להבחין בו מצורת המספר עצמו), ואם אין אלמנטים כלל, אז אי אפשר אפילו לכתוב אותו (אבל במקום זאת ניתן לסמן אותו ב- הערך שלו "0"). עם זאת, אם המונחים של הרצף מצוינים בדפוס מסוים, כגון פונקציה, אז אופרטור הסיכום יכול להיות שימושי או אפילו חיוני.
Record
כדי להבין מהו סכום, יש צורך גם לנתח את המראה שלו.
כדי לסכם רצף של מספרים שלמים מ-1 עד 100, לעתים קרובות נעשה שימוש בביטוי הכולל אליפסיס לציון האיברים החסרים: 1 + 2 + 3 + 4 + … + 99 + 100. התבנית היא די קל לראות בדוגמה זו. עם זאת, עבור אפשרויות מורכבות יותר, יש צורך לציין בדיוק את הכלל המשמש למציאת הערך של האלמנטים, אשר ניתן להשיג באמצעות אופרטור הסיכום "Σ". באמצעות סמל זה (סיגמא), אתה יכול להחיל את הסימון הבא:
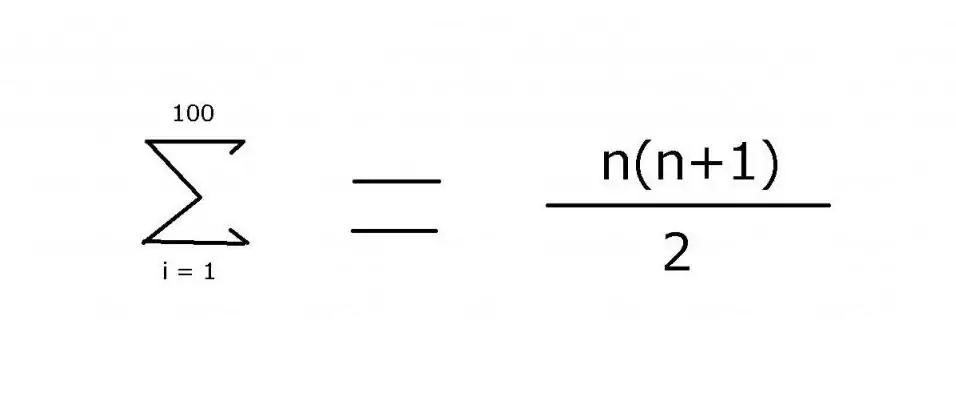
הערך של ביטוי זה הוא 5050. ניתן למצוא אותו באמצעות אינדוקציה מתמטית, שממנו הגיע החלק השני של הנוסחה.
עבור רצפים שונים, הנוסחה תשתנה. תהליך ההקלטה מצטמצם לחיפוש אחר התמונה המוקדמת של איזה רצף אינסופי ואז תיאורו באמצעות נוסחה. לאחר שעשית זאת, לא קשה להבין מה הסכום במקרה מסוים.
כשיש צורך להבהיר שמספרים מתווספים יחד עם הסימנים שלהם (פלוס או מינוס), משתמשים במונח סכום אלגברי. לדוגמה, בתורת המעגלים החשמליים, חוקי המעגלים של קירכהוף מתייחסים לסכום האלגברי של זרמים ברשת של מוליכים הנפגשים בנקודה, ונותנים סימנים מנוגדים לזרמים הזורמים פנימה ומחוצה לצומת.






