בפיסיקה, הנושא של חיבור מקביל וסדרה נחקר, והוא יכול להיות לא רק מוליכים, אלא גם קבלים. חשוב כאן לא להתבלבל לגבי איך כל אחד מהם נראה בתרשים. ורק אז ליישם נוסחאות ספציפיות. דרך אגב, אתה צריך לזכור אותם בעל פה.
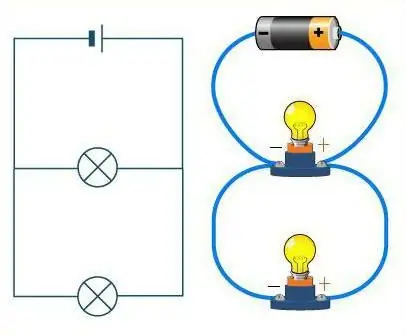
איך להבחין בין שני התרכובות האלה?
תסתכל מקרוב על הדיאגרמה. אם החוטים מיוצגים ככביש, המכוניות עליו ישחקו את התפקיד של נגדים. בכביש ישר ללא מזלגות, מכוניות נוסעות בזו אחר זו, בשרשרת. גם החיבור הסדרתי של מוליכים נראה אותו הדבר. לכביש במקרה זה יכול להיות מספר בלתי מוגבל של פניות, אך לא צומת אחד. לא משנה איך הכביש (החוטים) התנודד, המכונות (הנגדים) תמיד יהיו ממוקמות בזו אחר זו, בשרשרת אחת.
זה עניין אחר לגמרי אם נחשב חיבור מקביל. אז ניתן להשוות את הנגדים לספורטאים בהתחלה. הםכל אחד עומד על המסלול שלו, אבל יש להם אותו כיוון תנועה, וקו הסיום נמצא באותו מקום. באופן דומה, נגדים - לכל אחד מהם יש חוט משלו, אבל כולם מחוברים בשלב מסוים.
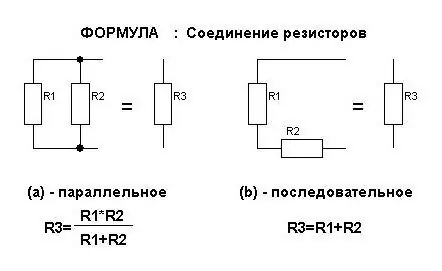
נוסחאות לחוזק הנוכחי
זה תמיד נדון בנושא "חשמל". חיבורים מקבילים וסדרתיים משפיעים על כמות הזרם בנגדים בדרכים שונות. עבורם, נגזרות נוסחאות שניתן לזכור. אבל מספיק רק לזכור את המשמעות שמושקעת בהם.
אז, הזרם בחיבור סדרתי של מוליכים הוא תמיד זהה. כלומר, בכל אחד מהם ערך החוזק הנוכחי אינו שונה. אתה יכול לצייר אנלוגיה אם אתה משווה חוט עם צינור. בו, מים זורמים תמיד באותה הדרך. וכל המכשולים בדרכו ייסחפו באותו כוח. אותו דבר עם הנוכחי. לכן, הנוסחה לזרם הכולל במעגל עם חיבור סדרה של נגדים נראית כך:
I gen=I 1=I 2
כאן, האות I מציינת את עוצמת הזרם. זהו סימון נפוץ, אז אתה צריך לזכור אותו.
הזרם בחיבור מקביל לא יהיה עוד ערך קבוע. עם אותה אנלוגיה לצינור, מסתבר שהמים יחולקו לשני זרמים אם לצינור הראשי יש ענף. אותה תופעה נצפית בזרם כאשר מופיעה הסתעפות של חוטים בדרכו. הנוסחה לחוזק הזרם הכולל כאשר המוליכים מחוברים במקביל:
I gen=I 1 + I 2
אם ההסתעפות מורכבת מחוטים שיותר משניים, אז בנוסחה שלמעלה יהיו יותר מונחים באותו מספר.
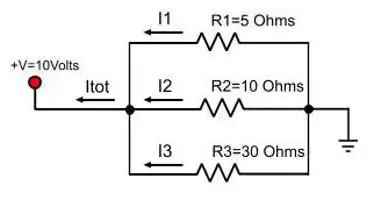
נוסחאות ללחץ
כאשר נחשב מעגל שבו המוליכים מחוברים בסדרה, המתח בכל הקטע נקבע על ידי סכום הערכים הללו בכל נגד ספציפי. אתה יכול להשוות מצב זה עם צלחות. לאדם אחד יהיה קל להחזיק אחד מהם, הוא יוכל לקחת גם את השני בקרבת מקום, אבל בקושי. אדם אחד כבר לא יוכל להחזיק שלוש צלחות אחת ליד השנייה, תידרש עזרה של שניה. וכו. המאמצים של אנשים מסתכמים.
הנוסחה עבור המתח הכולל של קטע של מעגל עם חיבור סדרה של מוליכים נראית כך:
U gen=U 1 + U 2, כאשר U הוא הייעוד שאומץ עבור מתח חשמלי.
מצב נוסף נוצר אם נחשב חיבור מקביל של נגדים. כאשר צלחות מוערמות זו על גבי זו, עדיין ניתן להחזיק אותן על ידי אדם אחד. אז אתה לא צריך להוסיף כלום. אותה אנלוגיה נצפית כאשר המוליכים מחוברים במקביל. המתח על כל אחד מהם זהה ושווה לזה שנמצא על כולם בבת אחת. הנוסחה למתח הכולל היא:
U gen=U 1=U 2
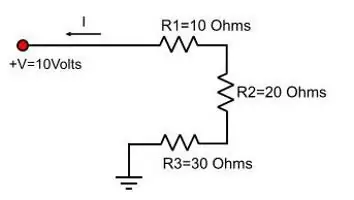
נוסחאות להתנגדות חשמלית
אי אפשר יותר לשנן אותם, אבל לדעת את הנוסחה של חוק אוהם ולהפיק ממנו את הרצוי. מחוק זה עולה כיהמתח שווה למכפלת הזרם וההתנגדות. כלומר, U=IR, כאשר R היא ההתנגדות.
אז הנוסחה שתצטרך לעבוד איתה תלויה באופן המחובר בין המוליכים:
- בסדרה, אז אתה צריך שוויון עבור מתח - IgenRtotal=I1R1 + I2R2;
- במקביל, יש צורך להשתמש בנוסחה לחוזק הנוכחי - Utotal / Rtotal=U 1/ R1 + U2 / R2 .
לאחר מכן טרנספורמציות פשוטות, שמתבססות על כך שבשוויון הראשון לכל הזרמים יש אותו ערך, ובשני - המתחים שווים. אז אפשר לקצר אותם. כלומר, מתקבלים הביטויים הבאים:
- R gen=R 1 + R 2 (לחיבור סדרתי של מוליכים)
- 1 / R gen=1 / R 1 + 1 / R 2(כאשר מחובר במקביל).
כאשר מספר הנגדים המחוברים לרשת גדל, מספר האיברים בביטויים אלו משתנה.
כדאי לציין שלחיבור מקבילי וסדרתי של מוליכים יש השפעה שונה על ההתנגדות הכוללת. הראשון שבהם מפחית את ההתנגדות של קטע המעגל. יתר על כן, מתברר שהוא פחות מהנגדים הקטן ביותר בשימוש. כאשר מחוברים בסדרה, הכל הגיוני: הערכים מסתכמים, כך שהמספר הכולל תמיד יהיה הגדול ביותר.
עבודה נוכחית
שלושת הכמויות הקודמות מרכיבות את חוקי החיבור המקביל וסידור הסדרות של מוליכים במעגל. לכן, חובה להכיר אותם. לגבי עבודה וכוח, אתה רק צריך לזכור את הנוסחה הבסיסית. כתוב כך: A \u003d IUt, כאשר A הוא עבודת הזרם, t הוא זמן המעבר שלו דרך המוליך.
כדי לקבוע את סך העבודה עם חיבור טורי, עליך להחליף את המתח בביטוי המקורי. אתה מקבל את השוויון: A \u003d I(U 1 + U 2)t, פותחים את הסוגריים שבהם מתברר שה העבודה על החלק כולו שווה לכמותם על כל צרכן שוטף ספציפי.
הנמקה מתקדמת באופן דומה אם נחשבת סכימת חיבור מקבילי. רק החוזק הנוכחי אמור להיות מוחלף. אבל התוצאה תהיה זהה: A=A 1 + A 2.
כוח נוכחי
בעת גזירת נוסחה להספק (סיימון "P") של קטע מעגל, אתה שוב צריך להשתמש בנוסחה אחת: P \u003d UI. לאחר נימוק כזה, מתברר שחיבורים מקבילים וסדרתיים הם מתואר על ידי נוסחה כזו לעוצמה: P \u003d P1 + P 2.
כלומר, לא משנה איך נערכו הסכמות, הכוח הכולל יהיה סכום המעורבים בעבודה. זה מסביר את העובדה שאי אפשר לכלול מכשירים חזקים רבים ברשת הדירות בו זמנית. היא פשוט לא יכולה לשאת את העומס.
איך משפיע חיבור המוליכים על תיקון זר השנה החדשה?
מיד אחרי שאחת הנורות נשרפת, מתברר איך הן היו מחוברות. בְּחיבור טורי, אף אחד מהם לא יידלק. זאת בשל העובדה שמנורה שהפכה לבלתי שמישה יוצרת שבר במעגל. לכן, אתה צריך לבדוק הכל כדי לקבוע איזה מהם נשרף, להחליף אותו - והזר יתחיל לעבוד.
אם הוא משתמש בחיבור מקביל, אז הוא לא מפסיק לעבוד אם אחת הנורות נכשלת. הרי השרשרת לא תישבר לגמרי, אלא רק חלק אחד מקביל. כדי לתקן זר כזה, אין צורך לבדוק את כל מרכיבי המעגל, אלא רק את אלו שאינם זוהרים.
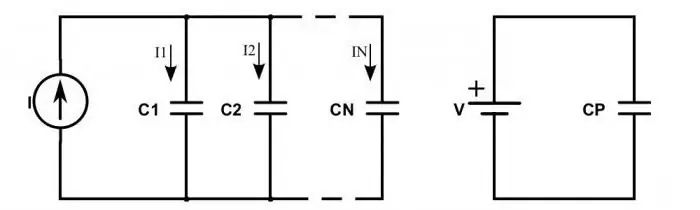
מה קורה למעגל אם כלולים קבלים במקום נגדים?
כאשר הם מחוברים בסדרה, נצפה המצב הבא: מטענים מהפלוסים של מקור הכוח מגיעים רק ללוחות החיצוניים של הקבלים הקיצוניים. אלה שביניהם פשוט מעבירים את המטען הזה לאורך השרשרת. זה מסביר את העובדה שאותם מטענים מופיעים בכל הלוחות, אבל עם סימנים שונים. לכן, ניתן לכתוב את המטען החשמלי של כל קבל המחובר בסדרה כך:
q gen =q 1=q 2.
כדי לקבוע את המתח על כל קבל, תצטרכו לדעת את הנוסחה: U=q / C. בה, C הוא הקיבול של הקבל.
המתח הכולל פועל לפי אותו חוק כמו נגדים. לכן, החלפת המתח בנוסחת הקיבול בסכום, נקבל שיש לחשב את הקיבול הכולל של המכשירים באמצעות הנוסחה:
C=q / (U 1 + U2).
תוכל לפשט את הנוסחה הזו על ידי הפיכת השברים והחלפת היחס בין מתח לטעינה בקיבול. מסתבר שהשוויון הבא: 1 / С=1 / С 1 + 1 / С 2.
המצב נראה שונה במקצת כאשר הקבלים מחוברים במקביל. אז המטען הכולל נקבע לפי סכום כל המטענים המצטברים על הלוחות של כל המכשירים. וערך המתח עדיין נקבע על פי חוקים כלליים. לכן, הנוסחה עבור הקיבול הכולל של קבלים המחוברים במקביל היא:
С=(ש 1 + ש' 2) / U.
כלומר, ערך זה נחשב כסכום של כל אחד מהמכשירים המשמשים בחיבור:
S=S 1 + S 2.
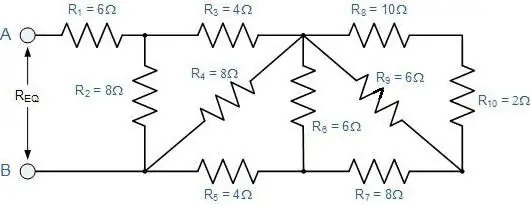
איך לקבוע את ההתנגדות הכוללת של חיבור שרירותי של מוליכים?
כלומר, כזה שבו קטעים עוקבים מחליפים את המקבילים, ולהיפך. מבחינתם, כל החוקים המתוארים עדיין תקפים. רק אתה צריך ליישם אותם בשלבים.
ראשית, זה אמור להרחיב מנטלית את התוכנית. אם קשה לדמיין את זה, אז אתה צריך לצייר מה קורה. ההסבר יתבהר אם נשקול אותו עם דוגמה ספציפית (ראה איור).
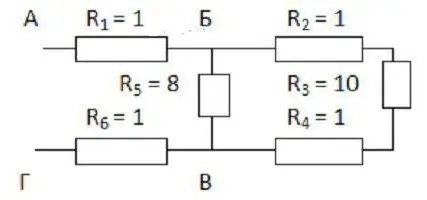
נוח להתחיל לצייר מנקודות B ו-C. יש למקם אותם במרחק מסוים אחד מהשני ומקצוות הגיליון. משמאל חוט אחד מתקרב לנקודה B, ושניים כבר מכוונים ימינה. לנקודה B, לעומת זאת, יש שני ענפים משמאל, וחוט אחד אחריה.
עכשיו אתה צריך למלא את החלל בין אלהנקודות. שלושה נגדים עם מקדמים של 2, 3 ו- 4 צריכים להיות ממוקמים לאורך החוט העליון, וזה עם אינדקס של 5 ילך מלמטה. שלושת הראשונים מחוברים בסדרה. עם הנגד החמישי הם במקביל.
שני הנגדים הנותרים (הראשון והשישי) מחוברים בסדרה עם הקטע הנחשב של ה-BV. לכן, ניתן פשוט להוסיף את הציור עם שני מלבנים משני הצדדים של הנקודות שנבחרו. נותר ליישם את הנוסחאות לחישוב ההתנגדות:
- תחילה זה שניתן לחיבור טורי;
- לאחר מכן עבור מקביל;
- ושוב ברציפות.
בדרך זו, אתה יכול לפרוס כל תוכנית, אפילו מורכבת מאוד.
בעיית החיבור הטורי של מוליכים
מצב. שתי מנורות ונגד מחוברים במעגל אחד מאחורי השני. המתח הכולל הוא 110 V והזרם הוא 12 A. מה הערך של הנגד אם כל מנורה מדורגת ב-40 V?
החלטה. מאחר ונבחן קשר סדרתי, הנוסחאות לחוקיו ידועות. אתה רק צריך ליישם אותם בצורה נכונה. התחל על ידי גילוי ערך המתח על פני הנגד. כדי לעשות זאת, אתה צריך להחסיר פעמיים את המתח של מנורה אחת מהסך הכל. מסתבר ש-30 V.
עכשיו כששתי כמויות ידועות, U ו-I (השנייה שבהן ניתנת בתנאי, מכיוון שהזרם הכולל שווה לזרם בכל צרכן סדרה), נוכל לחשב את ההתנגדות של הנגד באמצעות חוק אוהם. מסתבר שהוא 2.5 אוהם.
תשובה. ההתנגדות של הנגד היא 2.5 אוהם.
משימהלחיבור קבלים, מקבילים וסדרתיים
מצב. ישנם שלושה קבלים בעלי קיבולות של 20, 25 ו-30 מיקרופארד. קבע את הקיבול הכולל שלהם כאשר הם מחוברים בסדרה ובמקביל.
החלטה. קל יותר להתחיל עם חיבור מקביל. במצב זה, רק צריך להוסיף את כל שלושת הערכים. לפיכך, הקיבול הכולל הוא 75uF.
החישובים יהיו קצת יותר מסובכים כאשר קבלים אלה מחוברים בסדרה. אחרי הכל, תחילה עליך למצוא את היחס בין האחדות לכל אחת מהיכולות הללו, ולאחר מכן להוסיף אותן זו לזו. מסתבר שהיחידה חלקי הקיבולת הכוללת היא 37/300. אז הערך הרצוי הוא בערך 8 מיקרופארד.
תשובה. הקיבול הכולל בחיבור סדרתי הוא 8 uF, במקביל - 75 uF.






