לימוד התהליכים המתרחשים במערכות סטטיסטיות מסובך בגלל הגודל המינימלי של החלקיקים ומספרם העצום. זה כמעט בלתי אפשרי לשקול כל חלקיק בנפרד, ולכן מוצגות כמויות סטטיסטיות: המהירות הממוצעת של החלקיקים, הריכוז שלהם, מסת החלקיקים. הנוסחה המאפיינת את מצב המערכת, תוך התחשבות בפרמטרים מיקרוסקופיים, נקראת המשוואה הבסיסית של התיאוריה המולקולרית-קינטית של הגזים (MKT).
קצת על מהירות החלקיקים הממוצעת
קביעת מהירות החלקיקים בוצעה לראשונה בניסוי. ניסוי ידוע מתכנית הלימודים בבית הספר, שערך אוטו שטרן, איפשר ליצור רעיון של מהירויות החלקיקים. במהלך הניסוי נחקרה תנועת אטומי הכסף בגלילים מסתובבים: ראשית, במצב נייח של המתקן, לאחר מכן כאשר הוא מסתובב במהירות זוויתית מסוימת.
כתוצאה מכך, נמצא שמהירות מולקולות הכסף עולה על מהירות הקול והיא 500 מ'/שניה. העובדה היא די מעניינת, מכיוון שקשה לאדם להרגיש מהירויות כאלה של תנועה של חלקיקים בחומרים.
גז אידיאלי
המשך במחקרנראה שזה אפשרי רק במערכת שניתן לקבוע את הפרמטרים שלה על ידי מדידות ישירות באמצעות מכשירים פיזיים. מהירות נמדדת עם מד מהירות, אבל הרעיון של חיבור מד מהירות לחלקיק בודד הוא אבסורדי. ניתן למדוד ישירות רק פרמטר מקרוסקופי הקשור לתנועת חלקיקים.
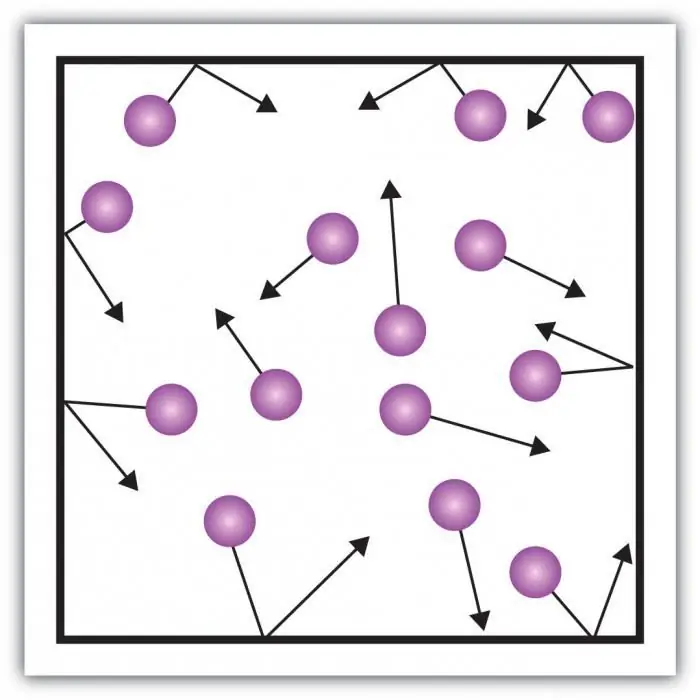
שקול לחץ גז. הלחץ על דפנות הכלי נוצר מההשפעות של מולקולות הגז בכלי. המוזרות של המצב הגזי של החומר היא במרחקים גדולים מספיק בין החלקיקים והאינטראקציה הקטנה שלהם זה עם זה. זה מאפשר לך למדוד ישירות את הלחץ שלו.
כל מערכת של גופים באינטראקציה מאופיינת באנרגיה פוטנציאלית ובאנרגיה קינטית של תנועה. גז אמיתי הוא מערכת מורכבת. השונות של האנרגיה הפוטנציאלית אינה מתאימה לשיטתיות. ניתן לפתור את הבעיה על ידי הצגת מודל הנושא את התכונות האופייניות של הגז, תוך טאטואציה הצידה את מורכבות האינטראקציה.
גז אידיאלי הוא מצב של חומר שבו האינטראקציה של חלקיקים זניחה, האנרגיה הפוטנציאלית של אינטראקציה שואפת לאפס. רק אנרגיית התנועה, התלויה במהירות החלקיקים, יכולה להיחשב משמעותית.
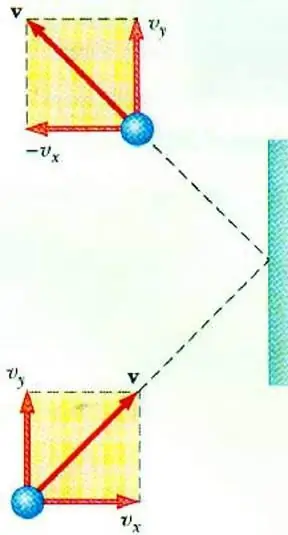
לחץ גז אידיאלי
כדי לחשוף את הקשר בין לחץ הגז למהירות החלקיקים שלו מאפשרת את המשוואה הבסיסית של MKT של גז אידיאלי. חלקיק שנע בכלי, בפגיעה בדופן, מעביר אליו דחף שאת ערכו ניתן לקבוע על סמך החוק השני.ניוטון:
F∆t=2m0vx
שינוי בתנע של חלקיק במהלך פגיעה אלסטית קשור לשינוי ברכיב האופקי של מהירותו. F הוא הכוח הפועל מצד החלקיק על הקיר למשך זמן קצר t; m0 - מסת חלקיקים.
כל חלקיקי הגז מתנגשים בפני השטח של שטח S במהלך הזמן ∆t, נעים בכיוון פני השטח במהירות vx וממוקמים בגליל בנפח Sυ x Δt. בריכוז החלקיקים n, בדיוק חצי מהמולקולות נעות לכיוון הקיר, החצי השני נע בכיוון ההפוך.
לאחר שקלטנו את ההתנגשות של כל החלקיקים, נוכל לכתוב את חוק ניוטון עבור הכוח הפועל על האזור:
F∆t=nm0vx2S∆t
מכיוון שלחץ הגז מוגדר כיחס בין הכוח הפועל בניצב לפני השטח לשטחו של האחרון, נוכל לכתוב:
p=F: S=nm0vx2
הקשר המתקבל כמשוואה הבסיסית של ה-MKT אינו יכול לתאר את המערכת כולה, מכיוון שרק כיוון תנועה אחד נחשב.
הפצה של Maxwell
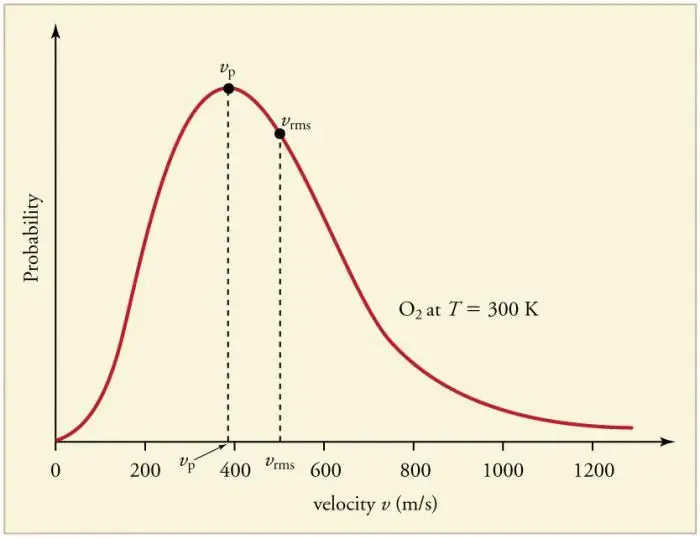
התנגשויות תכופות מתמשכות של חלקיקי גז עם הדפנות וביניהם מובילות לכינונה של התפלגות סטטיסטית מסוימת של חלקיקים במונחים של מהירויות (אנרגיות). הכיוונים של כל וקטורי המהירות מתבררים כסבירים באותה מידה. התפלגות זו נקראת התפלגות מקסוול. בשנת 1860 דפוס זה היהנגזר על ידי J. Maxwell על בסיס ה-MKT. הפרמטרים העיקריים של חוק ההפצה נקראים מהירויות: סביר, המקביל לערך המקסימלי של העקומה, ושורש-ממוצע-ריבוע vkv=√‹v2 › - הריבוע הממוצע של מהירות החלקיקים.
העלייה בטמפרטורת הגז תואמת לעלייה במהירות.
בהתבסס על העובדה שכל המהירויות שוות, ולמודולים שלהן יש אותו ערך, אנו יכולים להניח:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, מ: ‹ vx2›=‹v2›: 3
המשוואה הבסיסית של ה-MKT, תוך התחשבות בערך הממוצע של לחץ הגז, היא:
p=nm0‹v2›: 3.
קשר זה ייחודי בכך שהוא קובע את הקשר בין פרמטרים מיקרוסקופיים: מהירות, מסת חלקיקים, ריכוז החלקיקים ולחץ הגז באופן כללי.
באמצעות מושג האנרגיה הקינטית של חלקיקים, ניתן לשכתב את המשוואה הבסיסית של MKT אחרת:
p=2nm0‹v2›: 6=2n‹Ek›: 3
הלחץ של גז הוא פרופורציונלי לערך הממוצע של האנרגיה הקינטית של חלקיקיו.
טמפרטורה
מעניין, עבור כמות קבועה של גז בכלי סגור, אפשר לקשר בין לחץ הגז לבין הערך הממוצע של אנרגיית תנועת החלקיקים. במקרה זה, ניתן למדוד לחץ על ידי מדידת האנרגיהחלקיקים.
מה לעשות? איזה ערך ניתן להשוות לאנרגיה קינטית? הטמפרטורה מתגלה כערך כזה.

טמפרטורה היא מדד למצב התרמי של חומרים. כדי למדוד אותו, משתמשים במדחום, שבסיסו הוא ההתפשטות התרמית של נוזל העבודה (אלכוהול, כספית) בחימום. סולם מד החום נוצר בניסוי. בדרך כלל מניחים עליו סימנים התואמים את מיקומו של נוזל העבודה במהלך תהליך פיזי כלשהו המתרחש במצב תרמי קבוע (מים רותחים, קרח נמס). למדחום שונים יש סולמות שונים. לדוגמה, צלזיוס, פרנהייט.

סולם טמפרטורה אוניברסלי
מדי חום גז יכולים להיחשב מעניינים יותר מבחינת עצמאות מתכונות נוזל העבודה. קנה המידה שלהם אינו תלוי בסוג הגז המשמש. במכשיר כזה, אפשר להבחין באופן היפותטי בטמפרטורה שבה לחץ הגז שואף לאפס. חישובים מראים שערך זה מתאים ל-273.15 oC. סולם הטמפרטורה (סולם טמפרטורה אבסולוטי או סולם קלווין) הוצג ב-1848. הטמפרטורה האפשרית של לחץ גז אפס נלקחה כנקודה העיקרית של סולם זה. קטע יחידה של הסולם שווה לערך יחידה של סולם צלזיוס. נראה שנוח יותר לרשום את משוואת ה-MKT הבסיסית באמצעות טמפרטורה בעת לימוד תהליכי גז.
קשר בין לחץ וטמפרטורה
מבחינה אמפירית, אתה יכול לאמת זאתפרופורציונליות של לחץ הגז לטמפרטורה שלו. יחד עם זאת, נמצא כי הלחץ עומד ביחס ישר לריכוז החלקיקים:
P=nkT,
כאשר T הוא טמפרטורה מוחלטת, k הוא קבוע השווה ל-1.38•10-23J/K.
הערך היסודי, בעל ערך קבוע עבור כל הגזים, נקרא קבוע בולצמן.
בהשוואה בין תלות הלחץ בטמפרטורה לבין המשוואה הבסיסית של גזי MKT, נוכל לכתוב:
‹Ek›=3kT: 2
הערך הממוצע של האנרגיה הקינטית של תנועת מולקולות הגז הוא פרופורציונלי לטמפרטורה שלו. כלומר, הטמפרטורה יכולה לשמש כמדד לאנרגיה הקינטית של תנועת החלקיקים.






