חלק חשוב בתרמודינמיקה הוא חקר הטרנספורמציות בין שלבים שונים של חומר, שכן תהליכים אלו מתרחשים בפועל והם בעלי חשיבות מהותית לניבוי התנהגות מערכת בתנאים מסוימים. טרנספורמציות אלו נקראות מעברי פאזה, שאליהם מוקדש המאמר.
המושג של שלב ורכיב מערכת

לפני שממשיכים לשיקול של מעברי פאזה בפיזיקה, יש צורך להגדיר את מושג השלב עצמו. כידוע ממהלך הפיזיקה הכללית, ישנם שלושה מצבים של חומר: גזי, מוצק ונוזל. בחלק מיוחד במדע - בתרמודינמיקה - החוקים מנוסחים עבור שלבי החומר, ולא עבור מצבי הצבירה שלהם. שלב מובנה כנפח מסוים של חומר בעל מבנה הומוגני, מאופיין בתכונות פיזיקליות וכימיות ספציפיות ומופרד משאר החומר על ידי גבולות, הנקראים interphase.
לכן, המושג "פאזה" נושא מידע הרבה יותר משמעותי מבחינה מעשית על הנכסיםחומר מאשר מצב הצבירה שלו. לדוגמא, המצב המוצק של מתכת כגון ברזל יכול להיות בשלבים הבאים: מעוקב מרכז גוף מגנטי בטמפרטורה נמוכה (BCC), BCC לא מגנטי בטמפרטורה נמוכה, מעוקב במרכז פנים (fcc) ו-high- טמפרטורה לא מגנטי עותק מוסתר.
בנוסף למושג "פאזה", חוקי התרמודינמיקה משתמשים גם במונח "רכיבים", שפירושו מספר היסודות הכימיים המרכיבים מערכת מסוימת. המשמעות היא שהפאזה יכולה להיות חד-רכיבית (אלמנט כימי אחד) או רב-רכיבית (מספר יסודות כימיים).
משפט גיבס ושיווי משקל בין שלבי המערכת

כדי להבין מעברי פאזה, יש צורך לדעת את תנאי שיווי המשקל ביניהם. ניתן להשיג תנאים אלו באופן מתמטי על ידי פתרון מערכת משוואות גיבס עבור כל אחת מהן, בהנחה שמצב שיווי המשקל מושג כאשר אנרגיית הגיב הכוללת של המערכת המבודדת מהשפעה חיצונית מפסיקה להשתנות.
כתוצאה מפתרון מערכת המשוואות המצוינת, מתקבלים תנאים לקיומו של שיווי משקל בין מספר שלבים: מערכת מבודדת תחדל להתפתח רק כאשר הלחצים, הפוטנציאלים הכימיים של כל רכיב והטמפרטורות בכל השלבים שווים זה לזה.
כלל השלב של גיבס לשיווי משקל

מערכת המורכבת ממספר שלבים ורכיבים יכולה להיות בשיווי משקל לא רקבתנאים מסוימים, למשל, בטמפרטורה ולחץ ספציפיים. ניתן לשנות חלק מהמשתנים במשפט גיבס לשיווי משקל תוך שמירה על מספר השלבים ומספר הרכיבים הנמצאים בשיווי משקל זה. מספר המשתנים שניתן לשנות מבלי להפר את שיווי המשקל במערכת נקרא מספר החירויות של מערכת זו.
מספר החירויות l של מערכת המורכבת מפאזות ו-k רכיבים נקבע באופן ייחודי מכלל הפאזה של Gibbs. כלל זה כתוב מתמטית כך: l + f=k + 2. איך עובדים עם הכלל הזה? פשוט מאוד. למשל, ידוע שהמערכת מורכבת מ-f=3 שלבי שיווי משקל. מהו המספר המינימלי של רכיבים שמערכת כזו יכולה להכיל? אתה יכול לענות על השאלה על ידי נימוקים כדלקמן: במקרה של שיווי משקל, התנאים המחמירים ביותר קיימים כאשר הוא מתממש רק באינדיקטורים מסוימים, כלומר, שינוי בכל פרמטר תרמודינמי יוביל לחוסר איזון. המשמעות היא שמספר החירויות l=0. בהחלפת הערכים הידועים של l ו-f, נקבל k=1, כלומר מערכת שבה שלושה שלבים נמצאים בשיווי משקל יכולה להיות מורכבת ממרכיב אחד. דוגמה מצוינת היא הנקודה המשולשת של המים, שבה קרח, מים נוזליים וקיטור קיימים בשיווי משקל בטמפרטורות ולחצים ספציפיים.
סיווג של טרנספורמציות פאזה
אם אתה מתחיל לשנות כמה פרמטרים תרמודינמיים במערכת בשיווי משקל, אתה יכול לראות כיצד שלב אחד ייעלם ואחר יופיע. דוגמה פשוטה לתהליך זה היא המסת קרח כאשר הוא מחומם.
בהינתן שמשוואת Gibbs תלויה רק בשני משתנים (לחץ וטמפרטורה), ומעבר הפאזה כרוך בשינוי במשתנים אלה, אז מבחינה מתמטית ניתן לתאר את המעבר בין שלבים על ידי הבדלה של אנרגיית Gibbs ביחס לה. משתנים. בגישה זו השתמש הפיזיקאי האוסטרי פול ארנפסט בשנת 1933, כאשר ערכה סיווג של כל התהליכים התרמודינמיים הידועים המתרחשים עם שינוי בשיווי המשקל של השלבים.
מהיסודות של התרמודינמיקה נובע שהנגזרת הראשונה של אנרגיית גיבס ביחס לטמפרטורה שווה לשינוי באנטרופיה של המערכת. הנגזרת של אנרגיית גיבס ביחס ללחץ שווה לשינוי בנפח. אם, כשהשלבים במערכת משתנים, האנטרופיה או הנפח סובלים מהפסקה, כלומר משתנים בפתאומיות, אז הם מדברים על מעבר פאזה מסדר ראשון.
יתרה מכך, הנגזרות השניות של אנרגיית הגיבס ביחס לטמפרטורה וללחץ הן קיבולת החום ומקדם ההתפשטות הנפחית, בהתאמה. אם הטרנספורמציה בין שלבים מלווה בחוסר המשכיות בערכים של הכמויות הפיזיקליות המצוינות, אז מדברים על מעבר פאזה מסדר שני.
דוגמאות של טרנספורמציות בין שלבים

יש מספר עצום של מעברים שונים בטבע. במסגרת סיווג זה, דוגמאות בולטות למעברים מהסוג הראשון הן תהליכי המסת מתכות או עיבוי אדי מים מהאוויר, כאשר ישנה קפיצת נפח במערכת.
אם אנחנו מדברים על מעברים מסדר שני, אז דוגמאות בולטות הן הטרנספורמציה של ברזל ממצב מגנטי לפראמגנטי בטמפרטורה768 ºC או הפיכת מוליך מתכתי למצב מוליך על בטמפרטורות הקרובות לאפס המוחלט.
משוואות המתארות מעברים מהסוג הראשון
בפועל, לעתים קרובות יש צורך לדעת כיצד הטמפרטורה, הלחץ והאנרגיה הנספגת (השתחררת) משתנים במערכת כאשר מתרחשות בה טרנספורמציות פאזה. לשם כך נעשה שימוש בשתי משוואות חשובות. הם מתקבלים על סמך הידע של היסודות של התרמודינמיקה:
- הנוסחה של קלפיירון, הקובעת את הקשר בין לחץ וטמפרטורה במהלך טרנספורמציות בין שלבים שונים.
- נוסחת קלאוסיוס המקשרת בין האנרגיה הנספגת (השתחררה) לבין הטמפרטורה של המערכת במהלך הטרנספורמציה.
השימוש בשתי המשוואות אינו רק בהשגת תלות כמותית של כמויות פיזיקליות, אלא גם בקביעת הסימן של שיפוע עקומות שיווי המשקל בדיאגרמות פאזה.
משוואה לתיאור מעברים מהסוג השני

מעברי פאזה מהסוג הראשון והשני מתוארים באמצעות משוואות שונות, שכן היישום של משוואות קלאוזיוס וקלאוזיוס עבור מעברים מסדר שני מוביל לאי ודאות מתמטית.
כדי לתאר את האחרון, נעשה שימוש במשוואות Ehrenfest, המבססות קשר בין שינויים בלחץ ובטמפרטורה באמצעות ידע על שינויים בקיבולת החום ומקדם ההתפשטות הנפחית במהלך תהליך הטרנספורמציה. משוואות Ehrenfest משמשות לתיאור מעברי מוליך-על בהיעדר שדה מגנטי.
חשיבותדיאגרמות פאזה
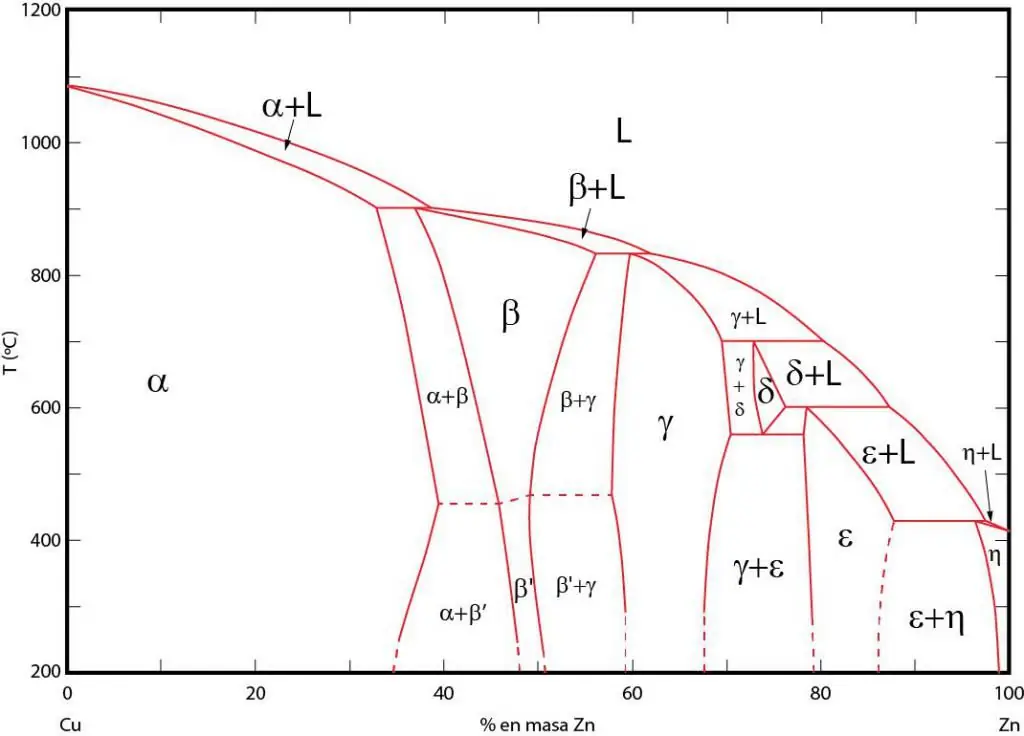
דיאגרמות פאזה הן ייצוג גרפי של אזורים שבהם השלבים התואמים קיימים בשיווי משקל. אזורים אלה מופרדים על ידי קווי שיווי משקל בין השלבים. לעתים קרובות נעשה שימוש בדיאגרמות פאזה P-T (לחץ-טמפרטורה), T-V (טמפרטורה-נפח) ו-P-V (נפח לחץ).
החשיבות של דיאגרמות פאזות נעוצה בעובדה שהם מאפשרים לחזות באיזה שלב תהיה המערכת כאשר התנאים החיצוניים ישתנו בהתאם. מידע זה משמש בטיפול בחום של חומרים שונים על מנת לקבל מבנה בעל תכונות רצויות.






