כאשר לומדים פיזיקה בכיתה י', נושא הדיפולים נחשב. מה המשמעות של מושג זה ובאילו נוסחאות משמשות לחישובו?
מבוא
אם תציבו דיפול במרחב של שדה חשמלי אחיד, תוכלו לייצג אותו כקווי כוח. דיפול הוא מערכת בה ישנם שני מטענים זהים בפרמטרים, אך הם מטענים נקודתיים מנוגדים. יתרה מכך, המרחק ביניהם יהיה הרבה פחות מהמרחק לכל נקודה בשדה הדיפול. מושג המומנט הדיפול נלמד בקורס האלקטרודינמיקה בבית הספר (כיתה י').
ציר הדיפול הוא קו ישר העובר בנקודות של שני המטענים. זרוע דיפול היא וקטור המחבר מטען ובו זמנית עובר מחלקיקים בעלי מטען שלילי לחלקיקים בעלי מטען חיובי. דיפול חשמלי מאופיין בנוכחות מצב כזה כמו דיפול או מומנט חשמלי.
לפי הגדרה, מומנט דיפול הוא וקטור ששווה מספרית למכפלת מטען הדיפול והזרוע שלו. יתר על כן, הוא מכוון יחד עם הכתף של הדיפול. בשוויון אפס של סכום הכוחות, אנו מחשבים את ערך הרגע. לזווית הקיימת בין מומנט הדיפול לביןכיווניות של השדה החשמלי, נוכחות של מומנט מכני אופיינית.
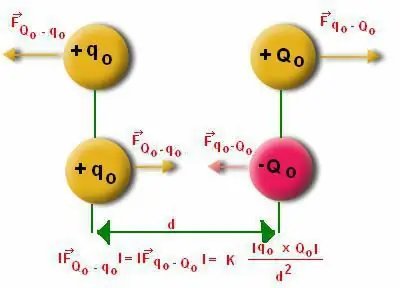
לעתים קרובות אנשים מתקשים לחשב את המודולוס הפועל על מבנה הדיפול. כאן יש צורך לקחת בחשבון את המוזרויות של חישוב הזווית "אלפא". ידוע שהדיפול סוטה מהמצב המאוזן. אבל לרגע הדיפול עצמו יש אופי משקם, מכיוון שהוא נוטה להיות בתנועה.
חישובים
כאשר מומנט דיפול זה ממוקם בתווך של שדה חשמלי לא-הומוגני, נוצר כוח בהכרח. בסביבה כזו, האינדיקטורים של סכום הכוחות לא יהיו אפס. כתוצאה מכך, ישנם כוחות הפועלים על מומנט הדיפול עם אופי נקודתי. הגודל של זרוע הדיפול קטן בהרבה.
ניתן לכתוב את הנוסחה כך: F=q (E2 - E1)=qdE, כאשר d הוא הפרש השדה החשמלי.
חפש את המאפיינים של המושג הפיזי הנחקר
בוא נסתכל על הנושא עוד יותר. על מנת לקבוע מהו המאפיין של השדה החשמלי, אם הוא נוצר באמצעות מערכת מטענים ומתמקם בחלל קטן, יש צורך לבצע מספר חישובים. דוגמה מוצגת על ידי אטומים ומולקולות, שבהרכבם יש גרעינים ואלקטרונים טעונים חשמלית.
אם יש צורך לחפש שדה במרחק גדול מהממדים המרכיבים את האזור בו נמצאים החלקיקים, נשתמש במספר נוסחאות מדויקות שהן מורכבות ביותר. אפשר להשתמש יותר פשוטביטויים משוערים. הבה נניח שקבוצות נקודתיות של מטענים qk לוקחות חלק ביצירת השדה החשמלי. הם ממוקמים בחלל קטן.
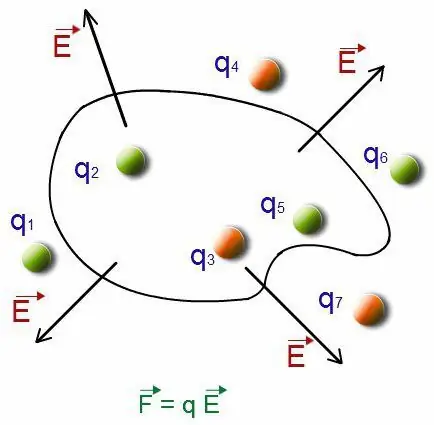
לביצוע חישוב המאפיין שיש לשדה, מותר לשלב את כל החיובים של המערכת. מערכת כזו נחשבת כמטען נקודתי Q. מחווני הגודל יהיו סכום המטענים שהיו במערכת המקורית.
מיקום החיובים
בוא נדמיין שמיקום המטען מצוין בכל מקום בו נמצאת מערכת החיובים qk. בעת ביצוע שינויים במיקום, אם יש לו גבולות המתבטאים בשטח קטן, השפעה כזו תהיה זניחה, כמעט בלתי מורגשת לשטח בנקודת המבט. בתוך גבולות כאלה של קירוב חוזק ופוטנציאל שיש לשדה החשמלי, קביעות נעשות באמצעות נוסחאות מסורתיות.
כאשר סכום המטען הכולל של המערכת הוא אפס, הפרמטרים של הקירוב המצוין ייראו גסים. זה נותן סיבה להסיק שהשדה החשמלי פשוט נעדר. אם יש צורך להשיג קירוב מדויק יותר, אסוף מחשבתית קבוצות נפרדות של מטענים חיוביים ושליליים של המערכת הנבדקת.
במקרה של תזוזה של ה"מרכזים" שלהם ביחס לאחרים, ניתן לתאר את פרמטרי השדה במערכת כזו כשדה שיש לו שני מטענים נקודתיים, שווים בגודלם ומנוגדים בסימן. יצוין כי הם עקורים ביחס לאחרים. לספקלאפיון מדויק יותר של מערכת המטענים מבחינת הפרמטרים של קירוב זה, יהיה צורך לחקור את תכונותיו של דיפול בשדה חשמלי.
מבוא למונח
בוא נחזור להגדרה. דיפול חשמלי הוא ההגדרה של מערכת שיש לה שני מטענים נקודתיים. יש להם אותו גודל וסימנים הפוכים. יתרה מכך, שלטים כאלה ממוקמים במרחקים קטנים יחסית לשלטים אחרים.
ניתן לחשב את המאפיין של התהליך שנוצר באמצעות דיפול, והוא מיוצג על ידי שני מטענים נקודתיים: +q ו-q, והם ממוקמים במרחק a יחסית לאחרות.

רצף החישובים
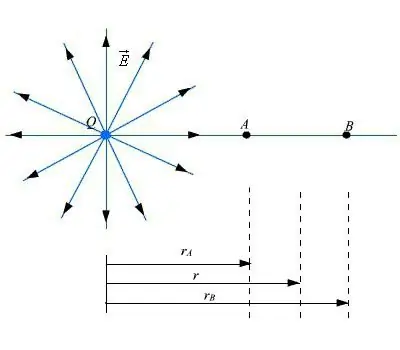
בוא נתחיל בחישוב הפוטנציאל והעוצמה שיש לדיפול על פני השטח הצירי שלו. זהו קו ישר שעובר בין שני מטענים. בתנאי שנקודה A ממוקמת במרחק השווה ל-r ביחס לחלק המרכזי של הדיפול, ואם היא r >> a, לפי עקרון הסופרפוזיציה לפוטנציאל השדה בנקודה זו, היא תהיה רציונלית ל השתמש בביטוי כדי לחשב את הפרמטרים של הדיפול החשמלי.
גודל וקטור החוזק מחושב לפי עקרון הסופרפוזיציה.לחישוב עוצמת השדה, נעשה שימוש במושג היחס בין פוטנציאל וחוזק שדה:
Ex=−Δφ /Δx.
בתנאים כאלה, כיוון וקטור העוצמה מצוין לאורך יחסית לציר הדיפול. כדי לחשב את המודולוס שלו, הנוסחה הסטנדרטית ישימה.
חשובהבהרות
יש לקחת בחשבון שההיחלשות של שדה הדיפול החשמלי מתרחשת מהר יותר ממה שהוא חווה מטען נקודתי. דעיכת פוטנציאל השדה הדיפולי עומדת ביחס הפוך לריבוע המרחק, ועוצמת השדה עומדת ביחס הפוך לקוביית המרחק.
באמצעות שיטות דומות, אך מסורבלות יותר, הפרמטרים של הפוטנציאל וחוזק השדה של הדיפול נמצאים בנקודות שרירותיות, שפרמטרי המיקום שלהן נקבעים באמצעות שיטת חישוב כזו כמו קואורדינטות קוטביות: המרחק ל- מרכז הדיפול החשמלי (r) והזווית (θ).
חישוב באמצעות וקטור מתח
המושג של וקטור העוצמה E מחולק לשתי נקודות:
- רדיאל (Er), המכוון בכיוון האורך ביחס לקו הישר.
- קו ישר כזה מחבר את הנקודה המצוינת ואת מרכז הדיפול עם האנך אליו Eθ.
פירוק זה של כל רכיב מכוון לאורך מהלך השינוי המתרחש עם כל הקואורדינטות של הנקודה שיש לצפות בה. אתה יכול למצוא אותו לפי היחס שמקשר בין מחווני חוזק שדה לשינויים פוטנציאליים.
למצוא את הרכיב הווקטור בחוזק השדה, חשוב לקבוע את אופי הקשר בשינויים הפוטנציאליים המתרחשים עקב תזוזה של נקודת התצפית לכיוון הוקטורים.
חשב את הרכיב הניצב
כשתסייםעבור הליך זה, חשוב לקחת בחשבון שהביטוי לגודל בתזוזה קטנה במאונך ייקבע על ידי שינוי הזווית: Δl=rΔθ.פרמטרי הגודל של רכיב שדה זה יהיו שווים.
לאחר קבלת היחס, אפשר לקבוע את השדה של הדיפול החשמלי בנקודה שרירותית כדי לבנות תמונה עם קווי הכוח של שדה זה.
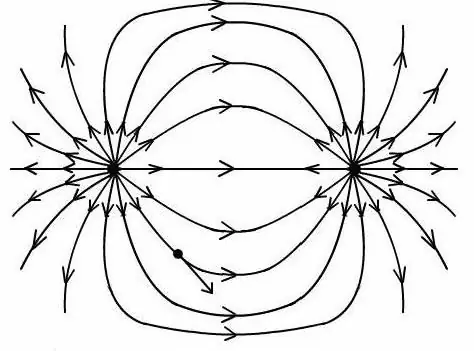
חשוב לקחת בחשבון שכל הנוסחאות לקביעת הפוטנציאל וחוזק השדה של דיפול פועלות רק על מכפלה של הערכים שיש למטען דיפול אחד והמרחק ביניהם.
רגע דיפול
כותרת העבודה המתוארת היא תיאור מלא של סוג המאפיינים החשמליים. יש לו את השם "מומנט דיפול של המערכת".
לפי הגדרת דיפול, שהוא מערכת של מטענים נקודתיים, ניתן לגלות שהוא מאופיין בנוכחות סימטריה צירית, כאשר הציר הוא קו ישר העובר במספר מטענים.
כדי להגדיר את המאפיין המלא של הדיפול, ציין את כיוון הכיוון שיש לציר. למען פשטות החישובים, ניתן לציין את וקטור מומנט הדיפול. ערך גודלו שווה לגודל מומנט הדיפול, וקטור הכיוון שונה על ידי צירוף המקרים שלו ושל ציר הדיפול. אז, p=qa אם a הוא הכיוון של הווקטור המחבר את המטען השלילי והחיובי של הדיפול.
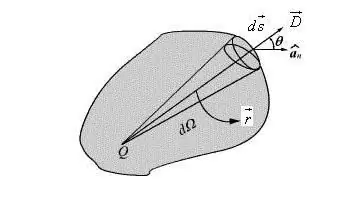
השימוש במאפיין כזה של הדיפול נוח ומאפשר ברוב המקרים לפשט את הנוסחה ולתת לה את הצורהוֶקטוֹר. תיאור הפוטנציאל של שדה הדיפול בנקודה של כיוון שרירותי כתוב בצורה של וקטור.
הכנסת מושגים כמו הווקטור המאפיין של דיפול ומומנט הדיפול שלו ניתנת לביצוע באמצעות מודל פשוט - מטען נקודתי בשדה אחיד, הכולל מערכת מטענים שמידותיה הגיאומטריות כן. לא חייבים לקחת בחשבון, אבל חשוב לדעת את רגע הדיפול. זהו תנאי מוקדם לביצוע חישובים.
איך מתנהג דיפול
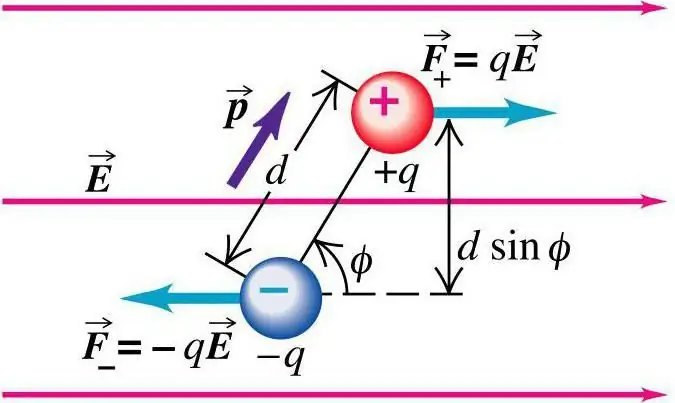
ניתן לראות את ההתנהגות של דיפול בדוגמה של מצב כזה. למיקום של שני מטענים נקודתיים יש אופי קבוע של מרחק זה ביחס לזה. הם הוצבו בתנאים של דיפול של שדה חשמלי אחיד. ערכו תצפיות על התהליך. בשיעורי הפיזיקה (אלקטרודינמיקה), מושג זה נשקל בפירוט. מהשדה למטען מתבצעת פעולת הכוחות:
F=±qE
הם שווים בגודלם ומנוגדים בכיוון. האינדיקטור של הכוח הכולל הפועל על הדיפול הוא אפס. מכיוון שלכוח כזה יש השפעה על נקודות שונות, הרגע הכולל יהיה:
M=Fa sin a=qEa sin a=pE sin a
כאשר α היא הזווית המחברת בין וקטורי עוצמת השדה לבין וקטורי מומנט דיפול. עקב נוכחותו של מומנט כוח, מומנט הדיפול של המערכת נוטה לחזור לכיווני וקטור חוזק השדה החשמלי.
דיפול חשמלי הוא מושג שחשוב להבין בבירור. אתה יכול לקרוא עוד על זה באינטרנט. גם זה יכולללמוד בשיעורי פיזיקה בבית הספר בכיתה י', כפי שדיברנו למעלה.






