תבניות או דפוסים גיאומטריים טבעיים מופיעים כצורות שחוזרות על עצמן שלעיתים ניתן לתאר או לייצג על ידי מודלים מתמטיים.
גיאומטריה בטבע ובחיים מגיעה בצורות וצורות רבות, כגון סימטריה, ספירלות או גלים.
היסטוריה
לראשונה, פילוסופים ומדענים יוונים עתיקים - פיתגורס, אמפדוקלס ואפלטון - התייחסו לשאלות של גיאומטריה בטבע. על ידי ניתוח דוגמאות של צורות גיאומטריות צפויות או אידיאליות בצמחים ובעלי חיים, הם ניסו להדגים סדר וסימטריה בטבע.
ניסיונות מודרניים לחקור גיאומטריה בטבע החלו במאה ה-19 עם מאמציו של הפיזיקאי הבלגי ג'וזף פלאטו, שפיתח את הרעיון של משטח המינימום של בועת סבון. הניסיונות המודרניים הראשונים התרכזו תחילה בהדגמת צורות גיאומטריות אידיאליות וניתנות לחיזוי, ולאחר מכן פנו לפיתוח מודלים המנבאים את המראה והביטוי של הגיאומטריה בטבע.
במאה ה-20, המתמטיקאי אלן טיורינג עבד על מנגנוני המורפוגנזה, מה שמסביר את ההופעה בבעלי חייםדוגמאות שונות, פסים, כתמים. מעט מאוחר יותר, הביולוגית אריסטיד לינדנמאייר, יחד עם המתמטיקאי בנואה מנדלברוט, ישלימו עבודה על פרקטלים מתמטיים שחזרו על דפוסי הצמיחה של כמה צמחים, כולל עצים.
Science
מדעים מודרניים (מתמטיקה, פיזיקה וכימיה), בעזרת טכנולוגיות ומודלים, נסו לא רק להסביר, אלא גם לחזות את התבניות הגיאומטריות המצויות בטבע.
הצורה והצבע של אורגניזמים חיים רבים, כמו טווס, יונקי דבש וקונכיות ים, הם לא רק יפים, אלא גם נכונים מבחינה גיאומטרית, מה שמושך את סקרנותם של מדענים. היופי שאנו רואים בטבע יכול להיגרם באופן טבעי, מתמטי.
הדפוסים הטבעיים הנצפים במתמטיקה מוסברים על ידי תורת הכאוס, הפועלת עם ספירלות ופרקטלים. דפוסים כאלה מצייתים לחוקי הפיזיקה, בנוסף, הפיזיקה והכימיה, תוך שימוש במתמטיקה מופשטת, מנבאים צורות של גבישים, טבעיים ומלאכותיים.
ביולוגיה מסבירה את הגיאומטריה בטבע על ידי ברירה טבעית, שבה ניתן להסביר מאפיינים קבועים כמו פסים, כתמים, צבעים בהירים על ידי הצורך במיסוך או שליחת אותות.
סוגי תבניות
בטבע, יש הרבה דפוסים חוזרים המופיעים בצורות גיאומטריות שונות. סוגי חוקיות בסיסית של גיאומטריה בטבע, תמונות ותיאוריהן ניתן למצוא להלן.
סימטריה. צורה גיאומטרית זו היא אחת הנפוצות בטבע. הנפוץ ביותר בבעלי חייםסימטריית מראה - פרפרים, חיפושיות, נמרים, ינשופים. הוא נמצא גם בצמחים, כמו עלי מייפל או פרחי סחלב. בנוסף, גיאומטריה סימטרית בטבע יכולה להיות רדיאלית, פי חמש או פי שישה, כמו פתיתי שלג.

פרקטלים. במתמטיקה, אלו מבנים דומים לעצמם שהם אינסופיים. בטבע, אי אפשר לזהות צורה אינסופית כזו שחוזרת על עצמה, לכן, קירובים של דפוסי פרקטלים נקראים פרקטלים גיאומטריים בטבע. ניתן לראות גיאומטריה כזו בטבע בעלי שרך, ברוקולי, פרי אננס.
ספירלות. צורות אלו נפוצות במיוחד בקרב רכיכות וחלזונות. מדענים צופים בצורות ספירליות בחלל, למשל, גלקסיות ספירליות. הספירלה נקראת יחס הזהב של פיבונאצ'י.

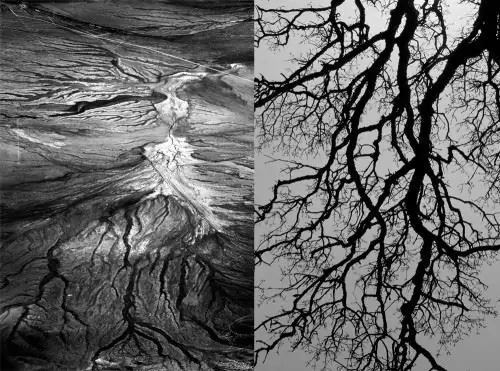
Meanders. האקראיות של מערכות דינמיות במתמטיקה מתבטאת בטבע בצורות כמו פיתולים וזרימות. גיאומטריה טבעית לובשת צורה של קו שבור או יותר נכון מעוקל, כגון זרימת נהר.
גלי. הם נגרמים על ידי הפרעות ותזוזות של אוויר, זרמי רוח, המתפשטים הן באוויר והן במים. בטבע לא מדובר רק בגלי ים, אלא גם בדיונות מדבריות, שיכולות ליצור צורות גיאומטריות - קווים, סהרונים ופרבולות.
פסיפס. נוצר על ידי חזרה על אותם אלמנטים על פני השטח. גיאומטריית פסיפס בחיות בר נמצאת אצל דבורים: הן בונותכוורת של חלות דבש - תאים חוזרים.

יצירת תבניות
בביולוגיה, היווצרות צבע גיאומטרי נובעת מתהליך הברירה הטבעית. עוד באמצע המאה ה-20 הצליח אלן טיורינג לתאר את המנגנון להופעת כתמים ופסים בצבע של בעלי חיים - הוא קרא לזה מודל התגובה-דיפוזיה. תאים מסוימים בגוף מכילים גנים הנשלטים על ידי תגובות כימיות. מורפוגן מוביל להיווצרות אזורי עור עם פיגמנט כהה (כתמים ופסים). אם המורפוגן קיים בכל תאי העור - מתקבל צבע הפנתר, אם הוא קיים בצורה לא אחידה - הנמר המנומר הרגיל.






