אפקטי תאורה אופייניים שכל אדם פוגש לעתים קרובות בחיי היומיום הם השתקפות ושבירה. במאמר זה נשקול את המקרה שבו שתי ההשפעות מתבטאות באותו תהליך, נדבר על תופעת השתקפות טוטאלית פנימית.
השתקפות אור
לפני ששוקלים את התופעה של השתקפות מוחלטת פנימית של אור, כדאי שתכירו את ההשפעות של השתקפות ושבירה רגילים. נתחיל עם הראשון. לשם הפשטות, נשקול רק אור, אם כי תופעות אלו אופייניות לגל מכל טבע.
השתקפות מובנת כשינוי של מסלול ישני אחד, שלאורכו נעה קרן אור, למסלול ישר אחר, כאשר היא נתקלת במכשול בדרכה. ניתן להבחין באפקט זה כאשר מפנים מצביע לייזר לעבר מראה. הופעת תמונות השמיים והעצים בהסתכלות על פני המים היא גם תוצאה של השתקפות אור השמש.

החוק הבא תקף להשתקפות: זוויותשכיחות והשתקפות נמצאים באותו מישור יחד עם האנך למשטח המשקף ושווים זה לזה.
שבירה של אור
השפעת השבירה דומה להחזר, רק שהיא מתרחשת אם המכשול בנתיב אלומת האור הוא מדיום שקוף אחר. במקרה זה, חלק מהקרן הראשונית מוחזר מהמשטח, וחלק עובר למדיום השני. החלק האחרון הזה נקרא קרן השבירה, והזווית שהוא עושה עם הניצב לממשק נקראת זווית השבירה. הקרן השבורה נמצאת באותו מישור כמו הקרן המשתקפת והנכנסת.
דוגמאות חזקות לשבירה הן שבירה של עיפרון בכוס מים או העומק המטעה של אגם כשאדם מסתכל למטה על קרקעיתו.

מתמטית, תופעה זו מתוארת באמצעות חוק Snell. הנוסחה המתאימה נראית כך:
1 sin (θ1)=n2 sin (θ) 2).
כאן זוויות הפגיעה והשבירה מסומנות כ-θ1 ו-θ2 בהתאמה. הכמויות n1, n2 משקפות את מהירות האור בכל מדיום. הם נקראים מדדי השבירה של המדיה. ככל ש-n גדול יותר, האור נע לאט יותר בחומר נתון. לדוגמה, במים מהירות האור קטנה ב-25% מאשר באוויר, ולכן מקדם השבירה עבורו הוא 1.33 (עבור אוויר הוא 1).
תופעת השתקפות פנימית מוחלטת
חוק שבירה של האור מוביל לאחדתוצאה מעניינת כאשר הקרן מתפשטת ממדיום עם n גדול. הבה נבחן ביתר פירוט מה יקרה לקורה במקרה זה. בואו נכתוב את הנוסחה של סנל:
1 sin (θ1)=n2 sin (θ) 2).
אנחנו נניח ש-n1>n2. במקרה זה, כדי שהשוויון יישאר אמיתי, θ1 חייב להיות קטן מ-θ2. מסקנה זו תקפה תמיד, מכיוון שרק זוויות מ-0o ל-90o נחשבות, ובתוכן פונקציית הסינוס הולכת וגדלה כל הזמן. לפיכך, כאשר משאירים מדיום אופטי צפוף יותר לתווך צפוף פחות (n1>n2), האלומה סוטה יותר מהרגיל.
עכשיו בואו נגדיל את הזווית θ1. כתוצאה מכך, יגיע הרגע שבו θ2 יהיה שווה ל-90o. מתרחשת תופעה מדהימה: קרן הנפלטת ממדיום צפוף יותר תישאר בה, כלומר עבורה הממשק בין שני חומרים שקופים יהפוך לאטום.
זווית קריטית
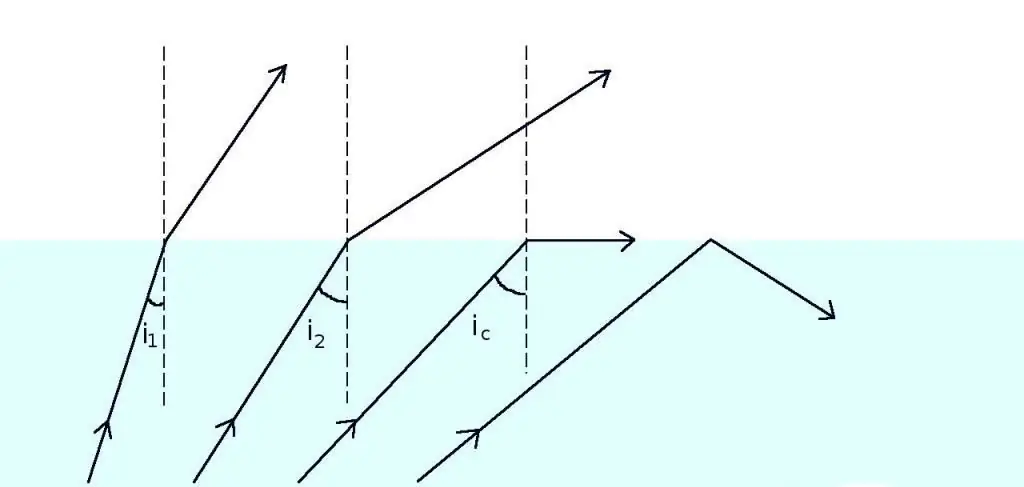
הזווית θ1, שעבורה θ2=90o, נקראת קריטי עבור צמד התקשורת הנחשב. כל קרן הפוגעת בממשק בזווית גדולה מהזווית הקריטית משתקפת לחלוטין לתוך המדיום הראשון. עבור הזווית הקריטית θc אפשר לכתוב ביטוי הנובע ישירות מהנוסחה של סנל:
sin (θc)=n2 / n1.
אםהמדיום השני הוא אוויר, ואז השוויון הזה מפושט בצורה:
sin (θc)=1 / n1.
לדוגמה, הזווית הקריטית למים היא:
θc=arcsin (1 / 1, 33)=48, 75o.
אם תצללו לקרקעית הבריכה ותביטו למעלה, תוכלו לראות את השמיים והעננים רצים על פניו רק מעל הראש שלכם, בשאר משטח המים ייראו רק קירות הבריכה.
מהנימוק לעיל, ברור שבניגוד לשבירה, השתקפות מוחלטת אינה תופעה הפיכה, היא מתרחשת רק כאשר עוברים ממדיום צפוף יותר למדיום פחות צפוף, אך לא להיפך.
השתקפות כוללת בטבע ובטכנולוגיה
אולי ההשפעה השכיחה ביותר בטבע, שאי אפשר בלי השתקפות מוחלטת, היא הקשת בענן. צבעי הקשת הם תוצאה של פיזור האור הלבן בטיפות גשם. עם זאת, כאשר הקרניים עוברות בתוך הטיפות הללו, הן חוות השתקפות פנימית בודדת או כפולה. לכן הקשת תמיד מופיעה כפולה.
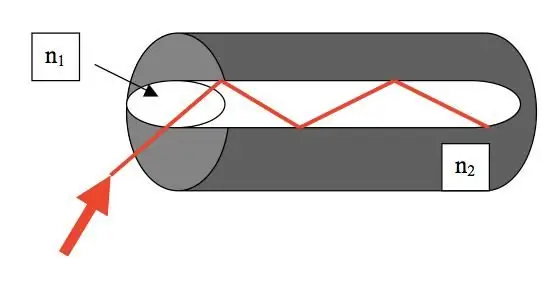
התופעה של השתקפות טוטאלית פנימית משמשת בטכנולוגיית סיבים אופטיים. הודות לסיבים אופטיים, ניתן לשדר גלים אלקטרומגנטיים ללא הפסד למרחקים ארוכים.






