אחת המשימות העיקריות של ניתוח מערכות בקרה דינמיות היא פתרון בעיית היציבות שלהן. היציבות שלהם היא אחד המאפיינים החשובים ביותר של תפיסת הניהול. המערכת נחשבת לא יציבה אם היא לא חוזרת למיקומה המקורי, אלא ממשיכה להתנודד לאחר שעברה שינויים מסוימים בכניסה, או שהיא תחת השפעת הפרעה לא רצויה.
הגדרת המושג הראשי
לפי תפיסת יציבות המערכת, מצב שיווי המשקל שלה נובע מהיעדר השפעת גורמים מטרידים עליה. במצב זה, ההבדל בין הסט למצב בפועל שואף לאפס. יציבות היא יכולתו לחזור למצב שיווי המשקל המקורי שלו לאחר שההפרעה שהובילה להפרתו הסתיימה. מערכת לא יציבה, עקב השפעתה של הפרעה, מתרחקת ממצב שיווי המשקל או מתנדנדת, שהמשרעת שלה בהדרגהעולה.

תנאי יציבות
למען יציבות של מערכת עם זמן קבוע, יש לעמוד בשני התנאים הבאים:
- היא תיצור פלט מוגבל עבור כל קלט; אם אין קלט, הפלט חייב להיות אפס, ללא קשר לתנאי ההתחלה.
- ניתן לקרוא ליציבות המערכת יציבות מוחלטת או יחסית. המונח המוצג משמש ביחס למחקר שבו משווים כמויות מסוימות, תנאי ההפעלה שלהן. יציבות היא התוצאה הסופית שנוצרה על ידי התוצאה.
אם הפלט של מערכת הוא אינסופי, אפילו כאשר מוחל עליה קלט סופי, ייאמר שהוא לא יציב, כלומר, יציב מטבעו, יש לו סיום מוגבל כאשר התחלה מוגבלת מוחלת על עצמו.
במקרה זה, הקלט מובן כנקודות יישום שונות של השפעת הסביבה החיצונית על המערכת. הפלט הוא התוצר הסופי של פעילותו, שהוא בצורה של נתוני הקלט שעברו טרנספורמציה.
במערכת זמן ליניארית רציפה, ניתן לכתוב את תנאי היציבות עבור תגובת דחף מסוימת.
כאשר הוא דיסקרטי, ניתן לכתוב את מדד היציבות גם עבור תגובת דחף מסוימת.
למצב לא יציב הן במערכות רציפות והן במערכות מוגבלות, הביטויים הללו יהיו אינסופיים.
סוגי יציבות והפרעות
תחת סטטייציבות המערכת מובנת כיכולתה להבטיח את שחזור המשטר המקורי (או קרוב למקור) לאחר הפרעה קטנה. על פי התפיסה המוצגת בהקשר זה, הם רואים בתנודה המשפיעה על התנהגותה, ללא קשר למקום בו מופיעים הזינוק או הנפילה ומה עוצמתם. בהתבסס על כך, מצבים אלה, שקרובים לזה ההתחלתי, מאפשרים לנו להתייחס אליו כלינארי.
יציבות דינמית של מערכות היא היכולת של האחרונות לשחזר את המצב ההתחלתי לאחר הפרעה גדולה.
תחת תנודה גדולה מובנת תנועה כזו, שאופי השפעתה והתנהגותה המקבילה קובעים את זמן קיום, גודל ומקום התרחשותה.
בהתבסס על זה, המערכת בטווח הזה מוגדרת כלא ליניארית.
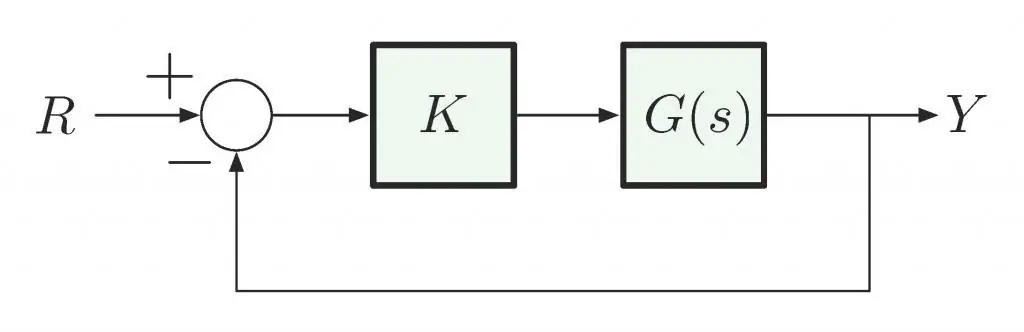
קריטריונים לקביעת קיימות
התנאי העיקרי ליציבותה של מערכת לינארית אינו אופי ההפרעה, אלא המבנה שלה. מאמינים שיציבות זו "בקטנה" נקבעת אם לא ייקבעו גבולותיה. היציבות "בגדול" נקבעת על פי הגבולות והתאמת הסטיות האמיתיות לגבולות שנקבעו אלה.
כדי לקבוע את יציבות המערכת, נעשה שימוש בקריטריונים הבאים:
- קריטריון שורש;
- קריטריון Stodola;
- קריטריון הורוויץ;
- קריטריון ניקוויסט;
- קריטריון מיכאילוב ואחרים
קריטריון השורש וטכניקת ההערכה של Stodola משמשים כדי לקבוע את היציבות של קישורים בודדיםומערכות פתוחות. קריטריון הורביץ הוא אלגברי ומאפשר קביעת יציבותן של מערכות סגורות ללא דיחוי. הקריטריונים של ניקוויסט ומיכאילוב הם תדירות. הם משמשים לקביעת היציבות של מערכות סגורות על סמך תגובת התדר שלהן.

קריטריון שורש
זה מאפשר לך לקבוע את יציבות המערכת, בהתבסס על צורת פונקציית ההעברה. תכונות ההתנהגות שלו מתוארות על ידי פולינום אופייני (המכנה של פונקציית ההעברה). אם נשווה את המכנה לאפס, שורשי המשוואה המתקבלת יאפשרו לנו לקבוע את מידת היציבות.
לפי קריטריון זה, המערכת הליניארית תהיה יציבה אם כל שורשי המשוואה נמצאים בחצי המישור השמאלי. אם לפחות אחד מהם ממוקם על גבול היציבות, הוא גם יהיה בגבול. אם לפחות אחד מהם נמצא בחצי המישור הימני, המערכת יכולה להיחשב כלא יציבה.
Criteria Stodola
זה נובע מהגדרת השורש. בהתאם לקריטריון סטודולה, מערכת ליניארית יכולה להיחשב יציבה אם כל המקדמים של הפולינום חיוביים.
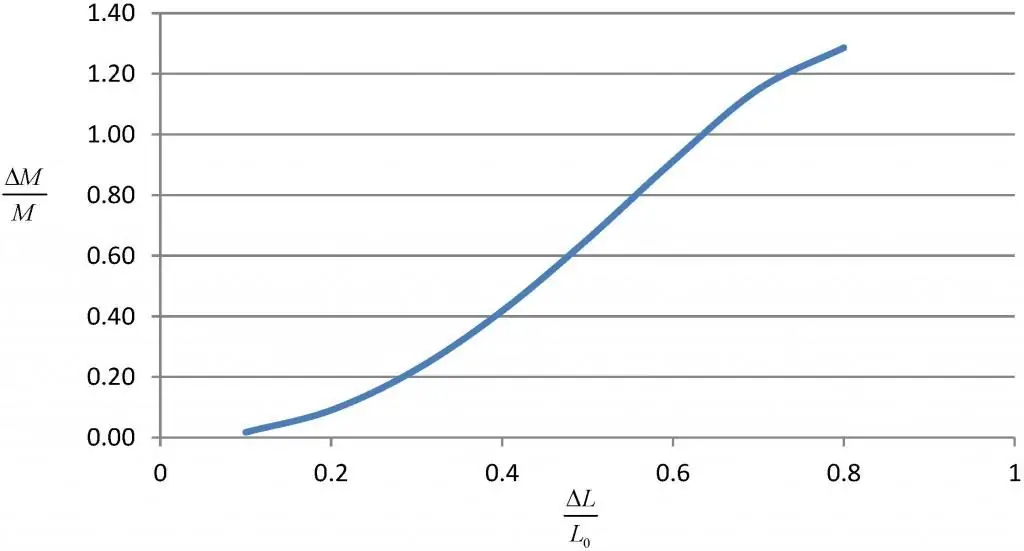
קריטריון הורוויץ
קריטריון זה משמש לפולינום המאפיין של מערכת סגורה. לפי טכניקה זו, תנאי מספיק ליציבות הוא העובדה שערך הקובע וכל מינור האלכסון העיקרי של המטריצה גדול מאפס. אם לפחות אחד מהם שווהאפס, זה נחשב על גבול היציבות. אם יש לפחות דטרמיננט שלילי אחד, יש לראות בו כלא יציב.
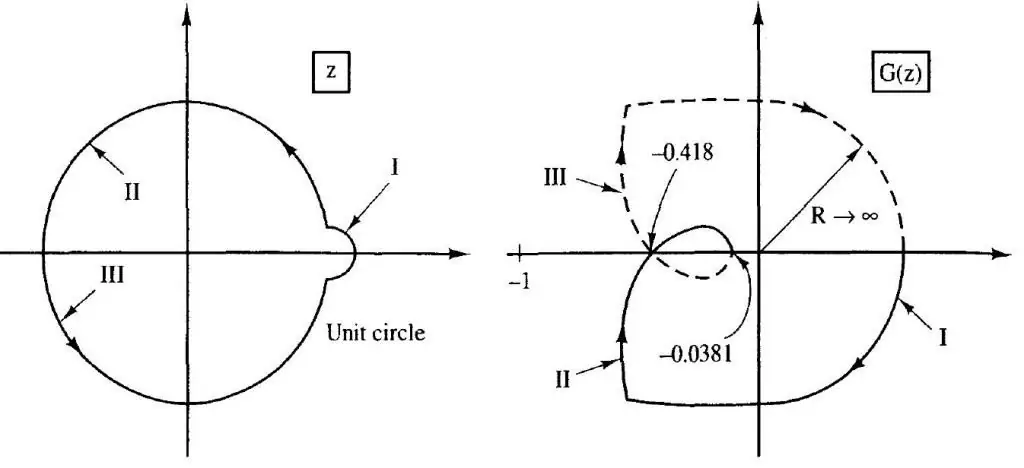
קריטריון ניקוויסט
הבסיס של טכניקה זו הוא בניית עקומה המחברת את הקצוות של וקטור של משתנה המציג את פונקציית ההעברה. הניסוח של הקריטריון הוא כדלקמן: מערכת סגורה נחשבת יציבה אם עקומת הפונקציה אינה מקיפה נקודה עם קואורדינטות (-1, j0) במישור המורכב.
מערכת איתנות פיננסית
חוסן פיננסי הוא המצב שבו המערכת, כלומר שווקים ומוסדות מרכזיים, עמידה בפני זעזועים כלכליים ומוכנה לבצע בצורה חלקה את תפקידי הליבה שלה: תיווך תזרים מזומנים, ניהול סיכונים והסדרי תשלום.
בגלל יחסי התלות ההדדיים של מתן פרשנות (הן אנכית והן אופקית), הניתוח חייב לכסות את כל מערכת התיווך הפיננסי. במילים אחרות, בנוסף למגזר הבנקאי יש צורך לנתח גם מוסדות חוץ בנקאיים העוסקים בתיווך בצורה כזו או אחרת. אלה כוללים סוגים רבים של מוסדות, לרבות חברות ברוקרים, קרנות השקעות, מבטחים וגופים אחרים (שונים). כאשר מנתחים מערכת של יציבות פיננסית, נלמדת עד כמה המבנה כולו מסוגל לעמוד בפני זעזועים חיצוניים ופנימיים. כמובן, זעזועים לא תמיד מביאים למשברים, אלא הסביבה הפיננסית הלא יציבה עצמהבפני עצמו יכול לעכב את ההתפתחות הבריאה של הכלכלה.
תאוריות שונות מזהות את הסיבות לחוסר יציבות פיננסית. הרלוונטיות שלהם עשויה להשתנות בהתאם לתקופה ולמדינות המעורבות בהיקף הניתוח. בין הגורמים הבעייתיים המשפיעים על המערכת הפיננסית כולה, הספרות מזהה בדרך כלל את הדברים הבאים:
- ליברליזציה מהירה של המגזר הפיננסי;
- מדיניות כלכלית לא מספקת;
- מנגנון שער חליפין לא ממוקד;
- הקצאה לא יעילה של משאבים;
- פיקוח חלש;
- רגולציה לא מספקת של חשבונאות וביקורת.
סיבות אפשריות מופיעות לא רק ביחד, אלא גם בנפרד או בשילוב אקראי, כך שניתוח היציבות הפיננסית הוא משימה קשה ביותר. ההתמקדות בענפים בודדים מעוותת את התמונה הגדולה, ולכן יש לקחת בחשבון את הנושאים במורכבותם במהלך לימודי היציבות הפיננסית.

תהליך ניתוח היציבות של המערכת הארגונית מתרחש במספר שלבים.
בתחילה, אינדיקטורים מוחלטים ויחסיים של יציבות פיננסית מוערכים ומנתחים. בשלב השני, הגורמים מחולקים בהתאם למשמעותם, השפעתם מוערכת מבחינה איכותית וכמותית.
יחס חוזק פיננסי של ארגונים
מצבה הפיננסי של החברה, יציבותה תלויה במידה רבה במבנה האופטימלי של מקורות ההון, כלומר, היחס בין החוב למשאבים העצמיים, במבנה האופטימלי.מבנה נכסי החברה ובראש ובראשונה על היחס בין הרכוש הקבוע והשוטף וכן יתרת הכספים וההתחייבויות של החברה.
לכן, חשוב ללמוד את מבנה מקורות ההון סיכון ולהעריך את מידת היציבות והסיכון הפיננסיים. למטרה זו, נעשה שימוש במקדמי יציבות המערכת:
- מקדם אוטונומיה (עצמאות) - חלק ההון במאזן;
- יחס תלות - חלקו של ההון הלווה במאזן;
- יחס חוב שוטף - היחס בין התחייבויות פיננסיות לטווח קצר למאזן;
- יחס יציבות פיננסית (עצמאות פיננסית לטווח ארוך) - היחס בין ההון והחוב לטווח ארוך למאזן;
- יחס כיסוי חוב (יחס כושר פירעון) - היחס בין הון לחוב;
- יחס מינוף פיננסי (יחס סיכון פיננסי) - היחס בין החוב להון.

ככל שרמת האינדיקטורים גבוהה יותר כגון אוטונומיה, יציבות פיננסית, כיסוי הון חוב, כך רמת קבוצת מקדמים אחרת (תלות, חוב שוטף, התחייבויות ארוכות טווח למשקיעים) נמוכה יותר, ובהתאם, יציבות מצבה הפיננסי של החברה. מינוף פיננסי נקרא גם מינוף פיננסי.






