גזים, מנקודת המבט של התרמודינמיקה, מתוארים על ידי קבוצה של מאפיינים מקרוסקופיים, שהעיקריים שבהם הם טמפרטורה, לחץ ונפח. הקביעות של אחד מהפרמטרים הללו והשינוי בשני האחרים מעידים על כך שמתרחש איזו-תהליך כזה או אחר בגז. נקדיש מאמר זה לתשובה מפורטת לשאלות שמדובר בתהליך איזוחורי, במה הוא שונה משינויים איזוטרמיים ואיזובריים במצבי מערכת גז.
גז אידיאלי בפיזיקה

לפני שתענה על השאלה שמדובר בתהליך איזוכורי, כדאי להכיר טוב יותר את המושג גז אידיאלי. בפיזיקה, הוא מובן ככל גז שבו האנרגיה הקינטית הממוצעת של החלקיקים המרכיבים אותו עולה בהרבה על האנרגיה הפוטנציאלית של האינטראקציה ביניהם, והמרחקים בין חלקיקים אלה גדולים בכמה סדרי גודל מהממדים הליניאריים שלהם. בתנאים שצוינו, זה אפשרי, בעת ביצועהחישובים אינם לוקחים בחשבון את אנרגיית האינטראקציה בין חלקיקים (היא שווה לאפס), וניתן גם להניח שהחלקיקים הם נקודות חומר בעלות מסה מסוימת m.
התהליך היחיד שמתרחש בגז אידיאלי הוא התנגשות של חלקיקים עם דפנות הכלי המכיל את החומר. התנגשויות אלו מתבטאות בפועל בקיומו של לחץ מסוים בגז P.
ככלל, כל חומר גזי המורכב ממולקולות אינרטיות כימית יחסית ושיש לו לחץ נמוך וטמפרטורות גבוהות יכול להיחשב כגז אידיאלי עם דיוק מספיק לחישובים מעשיים.
משוואה המתארת גז אידיאלי
כמובן, אנחנו מדברים על החוק האוניברסלי של קלפיירון-מנדלייב, שצריך להבין אותו היטב כדי להבין שזהו תהליך איזוחורי. אז, למשוואה האוניברסלית של המדינה יש את הצורה הבאה:
PV=nRT.
כלומר, המכפלה של הלחץ P ונפח הגז V שווה למכפלת הטמפרטורה המוחלטת T וכמות החומר במולות n, כאשר R הוא גורם המידתיות. המשוואה עצמה נכתבה לראשונה על ידי אמיל קלפיירון ב-1834, ובשנות ה-70 של המאה ה-19, ד' מנדלייב החליף בה קבוצה של ערכים קבועים של קבוע גז אוניברסלי יחיד R (8.314 J/(molK))).
בהתאם למשוואת קלפיירון-מנדלייב, במערכת סגורה מספר חלקיקי הגז נשאר קבוע, כך שיש רק שלושה פרמטרים מקרוסקופיים שיכולים להשתנות (T, Pו-V). העובדה האחרונה עומדת בבסיס ההבנה של תהליכי האיזו השונים שיידונו להלן.
מהו תהליך איזוכורי?
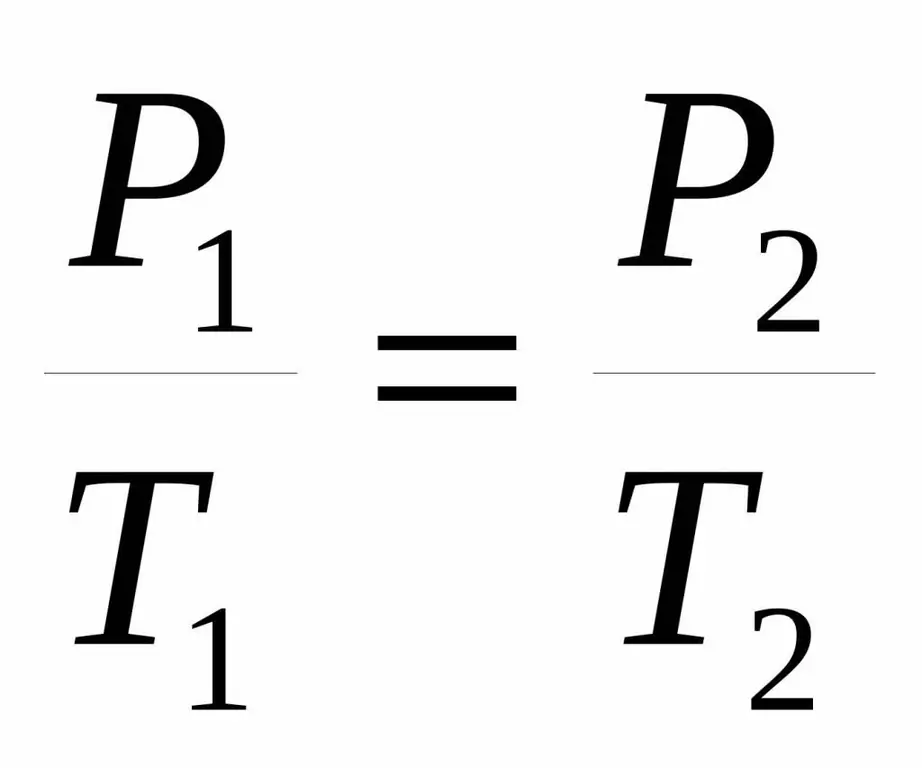
תהליך זה מובן כשינוי לחלוטין במצב המערכת, שבו הנפח שלה נשמר.
אם נפנה למשוואת המצב האוניברסלית, נוכל לומר שבתהליך איזוכורי רק לחץ וטמפרטורה מוחלטת משתנים בגז. כדי להבין בדיוק כיצד משתנים הפרמטרים התרמודינמיים, נכתוב את הביטוי המתמטי המתאים:
P / T=const.
לפעמים השוויון הזה ניתן בצורה מעט שונה:
P1 / T1=P2 / T 2.
שני השוויון נקראים חוק צ'ארלס על שמו של מדען צרפתי שבסוף המאה ה-18 השיג את התלות המצוינת בניסוי.

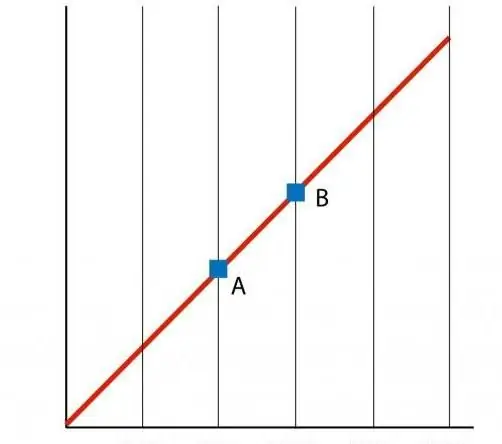
אם נבנה גרף של הפונקציה P(T), אז נקבל תלות בקו ישר, הנקראת איזוכור. כל איזוחור (עבור כל הערכים של n ו-V) הוא קו ישר.
תיאור אנרגיה של התהליך
כפי שצוין, תהליך איזוכורי הוא שינוי במצב של מערכת המתרחש במערכת סגורה אך לא מבודדת. אנחנו מדברים על אפשרות של חילופי חום בין הגז לסביבה. באופן כללי, כל אספקת חום Q למערכת מובילה לשתי תוצאות:
- changes אנרגיה פנימית U;
- גזהאם עובד A, הרחבה או התכווצות.
ההסקה האחרונה כתובה באופן מתמטי באופן הבא:
Q=U + A.
התהליך האיזוכורי של גז אידיאלי, לפי הגדרתו, אינו מרמז על עבודה שנעשתה על ידי הגז, שכן נפחו נותר ללא שינוי. המשמעות היא שכל החום המסופק למערכת הולך להגברת האנרגיה הפנימית שלה:
Q=U.
אם נחליף את הנוסחה המפורשת לאנרגיה פנימית בביטוי זה, אזי ניתן לייצג את החום של התהליך האיזוכורי כ:
Q=z / 2nRT.
כאן z הוא מספר דרגות החופש, אשר נקבע על פי האופי הפוליאטומי של המולקולות המרכיבות את הגז. עבור גז מונוטומי, z=3, עבור גז דו-אטומי - 5, ועבור טריאטומי ועוד - 6. כאן, תחת דרגות החופש, אנו מתכוונים לדרגות תרגום וסיבוביות.
אם נשווה את היעילות של חימום מערכת גז בתהליכים איזוחוריים ואיזובריים, אז במקרה הראשון נקבל את היעילות המקסימלית, שכן במהלך השינוי האיזוברי במצב המערכת, הגז מתרחב, ו חלק מתזונת החום מושקעת בביצוע עבודה.
תהליך איזוברי
לעיל תיארנו בפירוט שזהו תהליך איזוכורי. עכשיו בואו נגיד כמה מילים על איזו-תהליכים אחרים. נתחיל עם איזוברית. בהתבסס על השם, הוא מובן כמעבר של המערכת בין מצבים בלחץ קבוע. תהליך זה מתואר בחוק Gay-Lussac באופן הבא:
V / T=const.
כמו באיזושור, האיזובר V(T) מייצג גם קו ישר בגרף.
עבורמכל תהליך איזוברי, נוח לחשב את העבודה שעשה הגז, שכן היא שווה למכפלת הלחץ הקבוע והשינוי בנפח.
תהליך איזותרמי
זהו תהליך שבו הטמפרטורה של המערכת נשארת קבועה. זה מתואר על ידי חוק בויל-מריוט עבור גז אידיאלי. מעניין לציין שזהו חוק הגז הראשון שהתגלה בניסוי (המחצית השנייה של המאה ה-17). הסימון המתמטי שלו נראה כך:
PV=const.
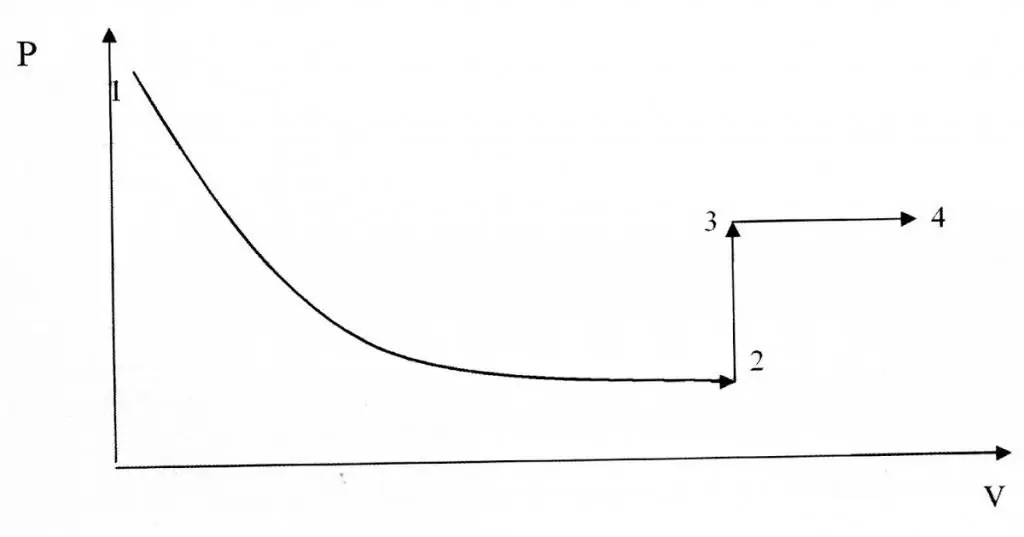
תהליכים איזוכוריים ואיזותרמיים נבדלים זה מזה מבחינת הייצוג הגרפי שלהם, מכיוון שהפונקציה P(V) היא קשר היפרבולי ולא ליניארי.
דוגמה לפתרון בעיות
בואו נאחד את המידע התיאורטי המסופק במאמר באמצעות היישום שלהם כדי לפתור בעיה מעשית. ידוע שחנקן גזי טהור היה בצילינדר בלחץ של 1 אטמוספירה ובטמפרטורה של 25 מעלות צלזיוס. לאחר חימום בלון הגז ונמדד הלחץ בו, התברר שהוא 1.5 אטמוספרות. מהי הטמפרטורה של הגז בצילינדר לאחר החימום? באיזו כמות השתנתה האנרגיה הפנימית של הגז אם היו 4 מולים של חנקן בבלון.
כדי לענות על השאלה הראשונה, אנו משתמשים בביטוי הבא:
P1 / T1=P2 / T 2.
מהמקום בו אנחנו מגיעים:
T2=P2 / P1 T 1.
בביטוי זה, ניתן להחליף לחץ ביחידות שרירותיותמידות, שכן הן מתכווצות, והטמפרטורה היא רק בקלווין. עם זאת, אנו מקבלים:
T2=1.5 /1298.15=447.224 K.
הטמפרטורה המחושבת במעלות צלזיוס היא 174 מעלות צלזיוס.
מכיוון שמולקולת החנקן היא דו-אטומית, ניתן לקבוע את השינוי באנרגיה הפנימית שלה במהלך החימום באופן הבא:
ΔU=5 / 2nRΔT.
החלפת הערכים הידועים בביטוי זה, נקבל את התשובה לשאלה השנייה של הבעיה: ΔU=+12.4 kJ.






